Nowcasting World Trade with Machine Learning: a Three-Step Approach

In a recent paper (available here), we nowcast world trade using machine learning methods. Two key lessons emerge. First, we distinguish machine learning between tree-based methods (random forest, gradient boosting) and their counterparts based on linear regressions (macroeconomic random forest, gradient linear boosting). While much less used in the literature, the latter are found to outperform not only the tree-based techniques, but also more “traditional” linear and non-linear techniques (OLS, Markov-switching, quantile regression). They do so significantly and consistently across different horizons and real-time datasets. Second, we propose a flexible three-step approach composed of (step 1) pre-selection, (step 2) factor extraction and (step 3) machine learning regression. Both pre-selection and factor extraction are found to significantly improve the accuracy of machine-learning-based predictions. This three-step approach also outperforms nowcasting workhorse models, such as PCA-OLS and dynamic factor model.

Why nowcasting with machine learning?

Real-time economic analysis often faces the fact that indicators are published with significant lags. This holds for world trade in volumes: the earliest estimates are published by the Centraal Plan Bureau (CPB) eight weeks after month end – meaning August data is available by October 25th. In the meantime, a number of early indicators are available. Our purpose is to exploit such information to get advance estimates of world trade ahead of the CPB releases. Based on the literature on forecasting trade, we identify a large dataset of 600 trade-related early indicators (e.g. PMI, retail sales, industrial production), and then use these variables to nowcast world trade, doing a horserace between traditional techniques and those based on machine learning.

The use of machine learning techniques responds to trade being highly volatile, much more than other macroeconomic variables like GDP or employment. In particular, trade growth tends to be very cyclical, with dramatic changes in crisis periods compared to normal times (see for example Bussiere et al., 2013). As this suggests the presence of non-linearities (e.g., threshold effects, regime switch, interactions), our idea is that using non-linear techniques could improve the accuracy of predictions. This drives us towards machine learning techniques, which can account for multiple types of non-linearities.

Does machine learning provide better accuracy?

Exploring over a range of machine learning techniques, a key ingredient in our paper is the distinction between tree-based and regression-based techniques. The first category – tree-based – includes random forest and gradient boosting. It is the most popular in the literature, notably random forests that have gained in popularity over recent years. The second category is an adaptation of the first but using linear regressions instead of, or in complement to, decision trees. It includes the macroeconomic random forest (Goulet-Coulombe, 2020) and the gradient linear boosting (Chen et al., 2016), two innovative methods that have received much less attention in the literature so far.

We find that machine learning techniques based on linear regressions outperform others significantly and consistently across different horizons, real-time datasets, and states of the economy. They first outperform the tree-based machine learning methods which – despite their popularity in the literature – perform poorly in our setup. This supports recent evidence that such techniques might be ill-equipped to deal with the short samples of time series in macroeconomics (e.g., Goehry, 2020). More broadly, we find that regression-based machine learning techniques also outperform more “traditional” techniques, both linear (OLS) and non-linear (Markov-switching, quantile regression). They do so again consistently and significantly – as found empirically by Diebold-Mariano and MCS tests).

Individually, the best-performing method is found to be the macroeconomic random forest of Goulet-Coulombe (2020), an extension of the canonical random forest. This is visible in Figure 1 which represents the accuracy (measured by the out-of-sample root mean squared errors, or RMSE, over 2012-2022) of the different techniques relative to OLS (= 1, figured by the black line). “Traditional” non-linear techniques (in shades of grey) and machine learning techniques based on trees (in shades of blue) fail to improve over the OLS benchmark (indicated by their RMSE above the black line). By contrast, machine learning techniques based on linear regressions (in shades of red) outperform the OLS benchmark by 15-20% on average – and therefore also outperform other non-linear techniques. Best in class is found to be the macroeconomic random forest (in dark red). Beyond the results presented in Figure 1, averaged over horizons and real-time datasets, evidence in our paper shows that these results hold true when considering individual horizons, real-time datasets, and states of the economy.

Figure 1: Accuracy of regression techniques relative to OLS


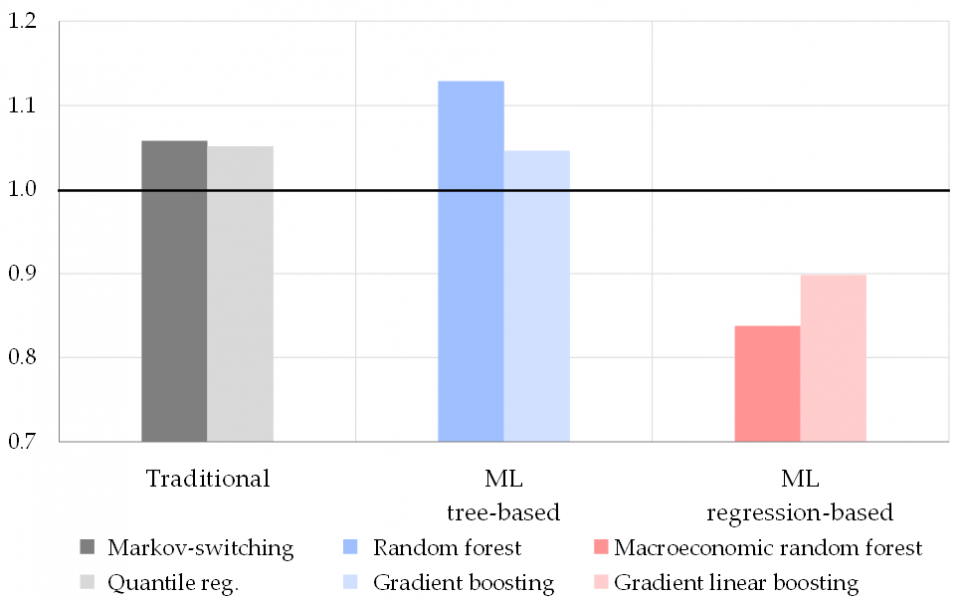
Notes: Accuracy is measured by the out-of-sample RMSE over Jan. 2012—Apr. 2022. Performances are presented relative to the OLS benchmark (black line). Results are obtained for the average of the datasets mirroring data available to a forecaster at the 1st, 11th, and 21st days of the month, and the average of the horizons at t-2, t-1, and t+1. The framework uses LARS for pre-selecting the 60 most informative regressors (out of 600 in our initial dataset), and factors extracted through PCA on the pre-selected set. Factors are then used as explanatory variables in the regressions. “ML tree-based” = machine learning techniques based on decision trees, “ML regression-based” = machine learning techniques based on linear regressions.

A flexible three-step approach

A second key contribution of our paper is to propose a three-step approach that maximizes the accuracy of forecasts based on machine learning and large datasets. The approach works sequentially: (step 1) a pre-selection technique identifies the most informative predictors; (step 2) selected variables are summarized and orthogonalized into a few factors; and (step 3) factors are used as explanatory variables in a regression using machine learning. It is motivated by the literature: Goulet-Coulombe et al. (2022) suggest that machine learning techniques are more accurate when used in a factor model. And doing pre-selection responds to another literature that found that selecting fewer but more informative regressors improves performance of factor models (Bai and Ng, 2008). Our framework combines these two strands and applies them to machine learning. We tested across a range of methods for each step and find that the best combination is given by the Least Angle Regression (LARS; Efron et al., 2004) for preselection, Principal Components Analysis (PCA) for factor extraction, and macroeconomic random forest for machine learning regression (see above).

Both pre-selection and factor extraction improve the accuracy of machine-learning-based predictions. In our setup, pre-selection enhances accuracy by around 10-15% on average. It suggests pre-selection can be useful for machine learning, despite the common idea that such techniques are able to handle large datasets with irrelevant variables. Similarly, summarizing into factors provides more accurate forecasts than using all individual variables as regressors, with accuracy gains also around 10-15% on average. This is shown in Figure 2 which presents the accuracy of the three-step approach relative to alternative setups where we skip either the pre-selection step (left panel) or the factor extraction step (right panel). In both cases, the accuracy of the three-step approach (coloured bars, corresponding to the different machine learning techniques) is better than the alternative when skipping one of the steps (black line at 1). Once again, results in Figure 2 are averaged across horizons and real-time datasets, but results by individual horizon and real-time dataset (available in the paper) yield similar conclusions.

Figure 2: Accuracy of three-step approach to alternative setup


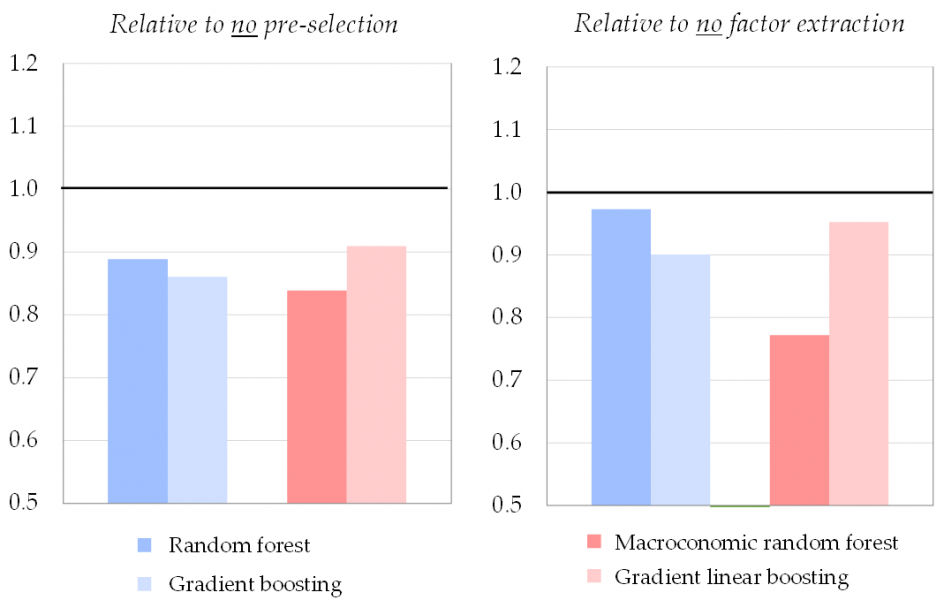
Notes: Accuracy is measured by the out-of-sample RMSE over Jan. 2012—Apr. 2022. Performances are presented relative to the alternative without either step (black line). Results are obtained for the average of the datasets mirroring data available to a forecaster at the 1st, 11th, and 21st days of the month, and the average of the horizons at t-2, t-1, and t+1. The framework uses LARS for pre-selecting the 60 most informative regressors (right panel) and factors extracted through PCA (left panel).

Finally, we compare the three-step approach to workhorse nowcasting techniques and find that it significantly outperforms them. It first outperforms the widely used “diffusion index” (Stock and Watson, 2002) that uses two steps: factors extraction via PCA and OLS regression on these factors. Compared to this method, the three-step approach can be viewed as an extension towards pre-selection and machine learning. Second, the three-step approach is also found to outperform a dynamic factor model based on quasi-maximum likelihood, notably at short horizons.

In conclusion, our experience offers two key lessons: (1) machine learning techniques based on regressions outperform machine learning techniques based on trees as well as other non-linear and linear techniques, and (2) pre-selection and factor extraction enhance accuracy of machine learning predictions. These lessons are best summarized in the three-step approach, which offers a practical and step-by-step method for forecasters willing to use (or at least to test) machine learning methods. To make this easier, we share a simplified version of our code on GitHub.