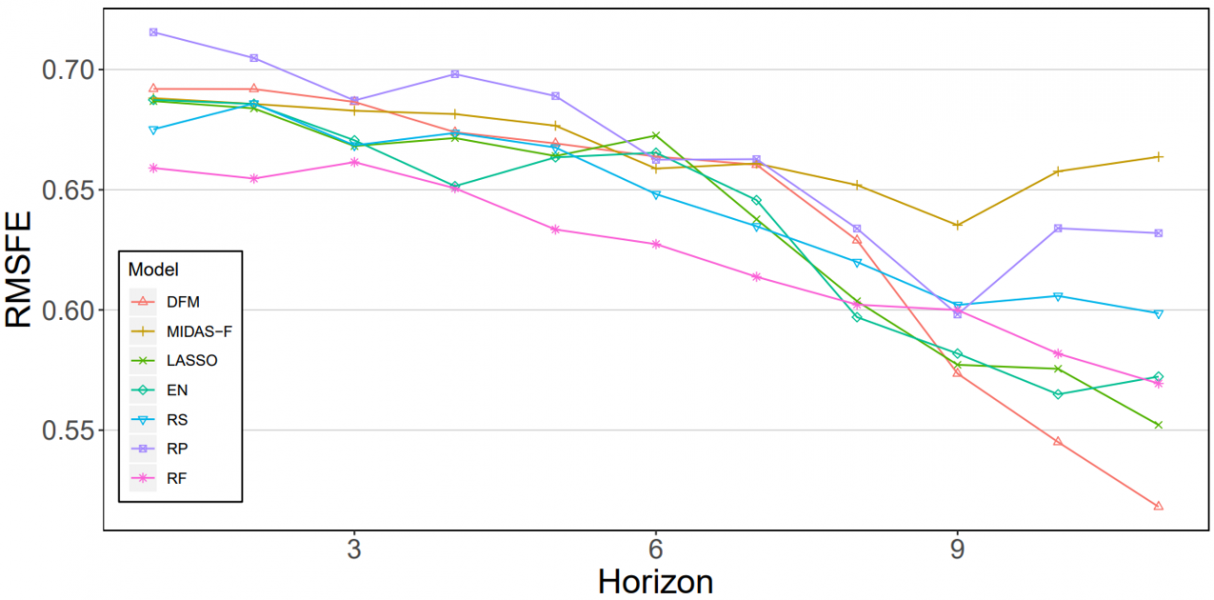
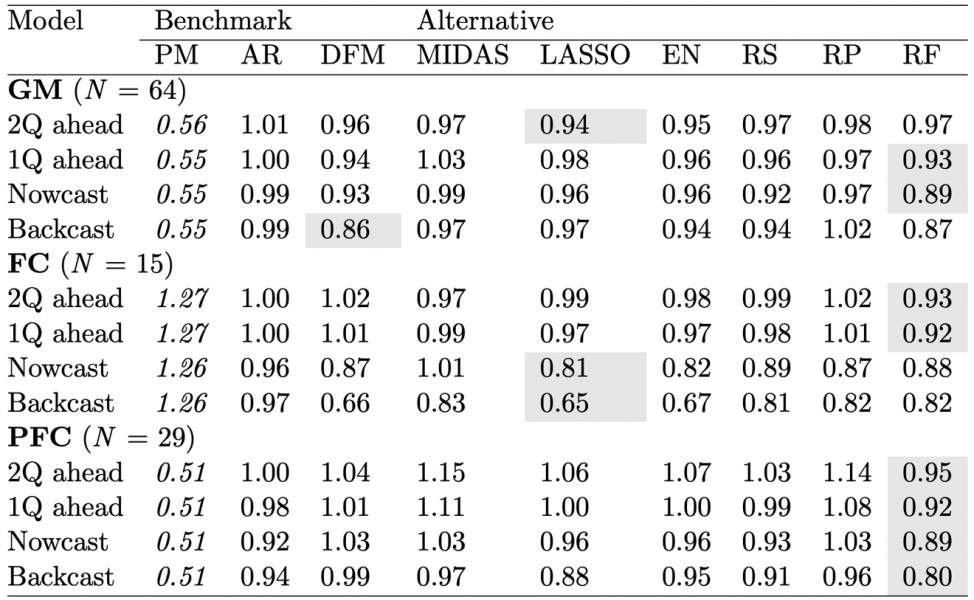
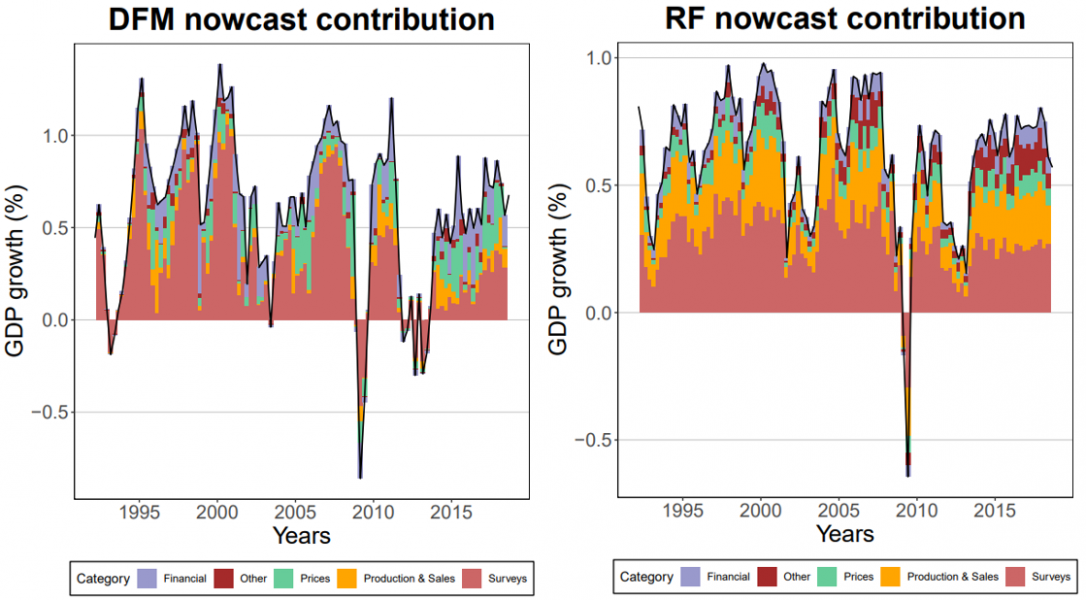
References
Banbura, M., and G. Rünstler (2011) A look into the factor model black box: Publication lags and the role of hard and soft data in forecasting GDP. International Journal of Forecasting, 27: 333-346
Bok B., D. Caratelli, D. Giannone, A. Sbordone, and A. Tambalotti (2018) Macroeconomic nowcasting and forecasting with big data. Annual Review of Economics, 10: 615-643
Kant, D., A. Pick, and J. de Winter (2022) Nowcasting GDP using machine learning methods. DNB Working Paper 754