CBDC Policies in Open Economies

Author(s): Michael Kumhof, Marco Pinchetti, Phurichai Rungcharoenkitkul, Andrej Sokol

Date published: May 2023

SUERF Policy Brief, No 587*

By Michael Kumhof (CEPR), Marco Pinchetti (Centre for Macroeconomics), Phurichai Rungcharoenkitkul (BIS and Bank of Thailand), and Andrej Sokol (Bloomberg)

*The views expressed in this paper are those of the authors and should not be attributed to the institutions with which the authors are affiliated.

JEL codes: E41, E42, E43, E44, E52, E58, F41.
Keywords: Central bank digital currencies, monetary policy, bank deposits, bank loans, monetary frictions, money demand, money supply, credit creation.

Download: SUERF Policy Brief, No 587 (1.51 MB)

We study the introduction of interest-bearing retail CBDC, competing with bank deposits as medium of exchange, into an estimated 2-country DSGE environment. An increase in the CBDC interest rate is expansionary. A CBDC issuance of 30% of GDP increases steady state output and welfare by 6% and 2%. Financial shocks account for half of the variance of aggregate demand and inflation, and for most of the variance of financial variables. Compared to a conventional baseline, there are welfare gains of 0.57% from a more aggressive Taylor rule, of another 0.44% from an optimized CBDC interest rate rule that responds to a credit gap, and of another 0.57% if the latter is accompanied by automatic fiscal stabilizers. A CBDC quantity rule, a response to an inflation gap, CBDC as retail access to reserves, and especially a cash-like zero-interest CBDC, yield significantly smaller gains. CBDC policies can reduce the volatilities of capital flows and of the exchange rate by around one third.

Central banks worldwide are actively studying the possibility of issuing digital money to the public, a concept that has become known as central bank digital currencies, or CBDC. While the microeconomic and technological benefits of CBDC have so far received most of the attention in the ongoing policy discussion, many macroeconomic aspects of CBDC policies remain underexplored. We aim to fill this gap, by providing answers to three questions. First, what are the consequences of a hypothetical transition between a pre-CBDC and a post-CBDC economy? Second, how should central banks design CBDC policy rules, jointly with traditional monetary policy or Taylor rules? Third, what are the open economy implications of CBDC?

CBDC in our Model

Our analysis relies on four assumptions about the architecture and design features of CBDC. First, we focus on the retail variety of CBDC that is accessible to both non-banks and banks. Second, non-banks are able to hold CBDC (and bank deposits) in both currencies. Third, retail CBDC is remunerated at an interest rate that, because CBDC also provides retail liquidity services, is substantially below the interest rate on wholesale central bank reserves.1 Fourth, the central bank unconditionally guarantees CBDC issuance only against government bonds. While the conversion of bank deposits into CBDC at the central bank may in practice take place at most times, it remains discretionary. This helps to prevent system-wide runs from bank deposits into CBDC (Kumhof and Noone (2021)).

The Analytical Framework

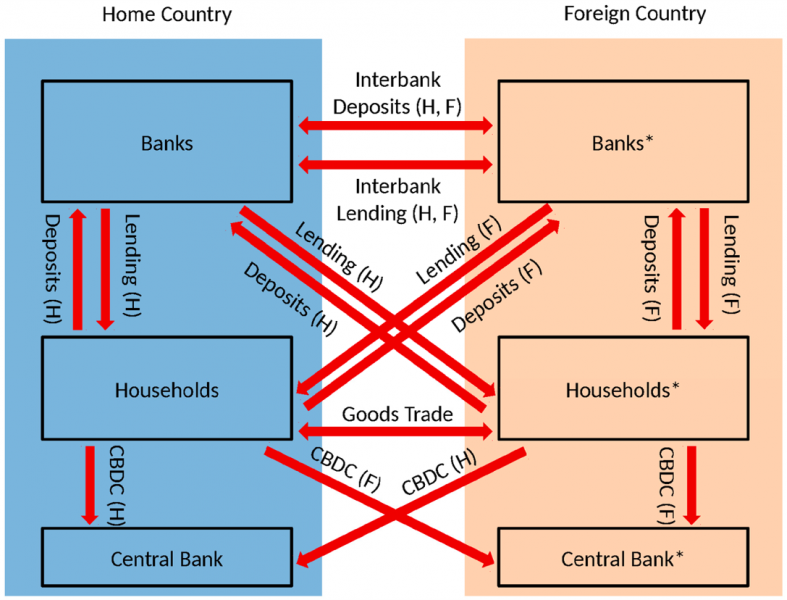
Our model features 2 countries, and in our quantitative implementation we think of these as the US and the rest of the world. Pre-CBDC, the medium of exchange function is performed by deposits that are created by banks through collateralised loans. Post-CBDC, it is performed jointly by deposits and CBDC, the latter issued by the central bank against government bonds. The two are imperfect substitutes. Domestic and cross-border gross capital flows arise because non-banks demand CBDC and bank deposits in both currencies, and because domestic banks only issue loans and deposits in domestic currency. A schematic representation of our model is shown in Figure 1.

Figure 1: Domestic and Cross-Border Gross Financial and Real Flows

The pre-CBDC model’s steady state is calibrated, and its dynamic and policy rule parameters are estimated, using quarterly US data from 1990Q1 to 2019Q4. We then carry out a number of policy experiments. The transition simulation, which abstracts from uncertainty, assumes the overnight issuance of CBDC equal to 30% of GDP in one country, against an equal amount of government bonds, and traces the effects on the macro-economy over the long as well as the short run. The CBDC policy rules exercises, which apply the estimated standard errors and persistence of shocks to post-CBDC economies with different types of CBDC policy rules, evaluate the welfare consequences of different specifications and parameterisations of the policy rules. The open economy aspects are studied by examining the response of cross-border capital flows and exchange rates to different policy rules.

Estimation

We find that financial shocks, which affect either the supply of or the demand for money, account for around half of the volatility of aggregate demand and inflation, and for the bulk of the volatility of balance sheets, spreads, and the exchange rate. This matters because, while conventional Taylor rules are particularly effective at smoothing the effects of real business cycle shocks through an intertemporal substitution channel, CBDC policy rules are particularly effective at smoothing the effects of financial shocks through a money supply channel.

Transition

We find strong positive effects of a transition from a pre-CBDC to a post-CBDC economy, with long-run output gains of just under 6% and long run welfare gains of just over 2% of steady state consumption, due to a combination of lower real interest rates, lower distortionary taxes, and lower monetary frictions. The main short-run and long-run effects are illustrated in Figure 2.

Figure 2: Impacts of Transition to a CBDC Economy

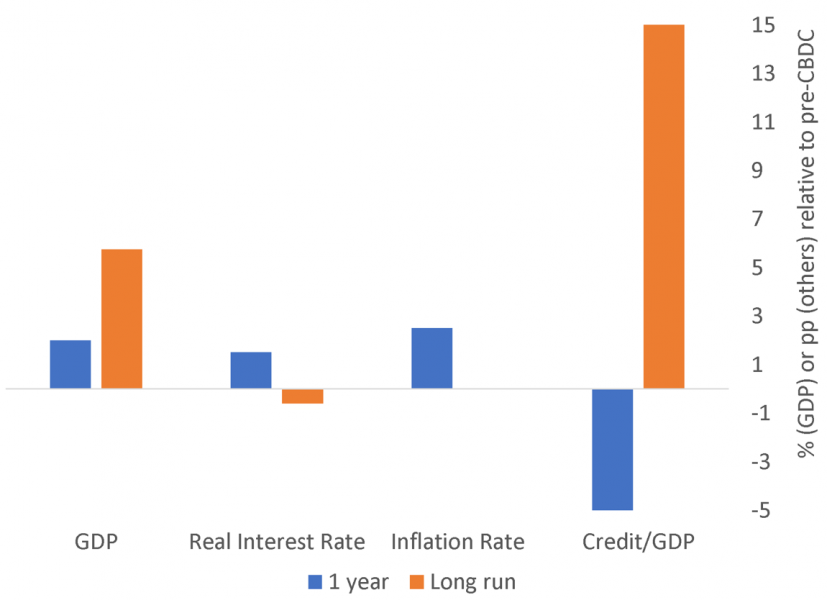
Real interest rates, and fiscal spending on interest charges, drop in the long run. This is both because CBDC carries a much lower interest rate due to its monetary convenience yield, and because CBDC is not defaultable2, so that its issuance against defaultable government debt reduces sovereign interest rate premia. During a short transition period the real policy interest rate rises, because the introduction of CBDC initially stimulates demand by more than supply, thereby driving up inflation and triggering a policy response. Taxes on labor, capital and consumption drop both immediately and, even more strongly, in the long run, because the reduction in fiscal spending on interest charges, together with unchanged government spending, creates fiscal space to do so. Monetary frictions (which one can think of as one of the costs of doing business) are reduced because CBDC allows non-banks, at least to some extent, to satisfy their need for a medium of exchange in a less costly manner than through bank deposits. The overall money supply thus increases, bringing the economy closer to the Friedman (1969) rule ideal, which states that the money supply should be expanded to the point where the marginal benefit of money equals its marginal cost.

Banks are not crowded out by CBDC, except modestly during a short transition period that need not even occur if CBDC is introduced more gradually than in our simulation. Bank balance sheets grow significantly in the long run (by around 15% of GDP), due to increased demand for all types of money balances in a growing economy. Banks’ average funding cost remains approximately constant despite greater bank reliance on wholesale funding, due to the reduction in sovereign interest rate premia.

CBDC Policy Rules

A fundamental insight of our work is that, because CBDC is a medium of exchange, in a recession the central bank should raise rather than lower the CBDC interest rate relative to the interest rate on reserves. The reason is that this reduces the opportunity cost of holding CBDC, which increases the equilibrium quantities of CBDC and of overall money, and this in turn reduces monetary frictions. The final result is a stimulus to both aggregate supply (to the extent that money is used to purchase inputs into production) and aggregate demand (to the extent that money is used to purchase consumption or investment goods). This money supply transmission channel of CBDC can help to stabilize inflation and output alongside the traditional intertemporal substitution channel of the Taylor rule.

We find that, as long as the government runs a balanced budget fiscal rule (with lump-sum taxes), the best combination of Taylor and CBDC rules can achieve a welfare gain of 1.01% relative to a conventional baseline that features (i) a Taylor rule with an inflation gap coefficient of 1.5 and a small output growth coefficient, and (ii) a CBDC interest rate rule that maintains at a fixed spread between the interest rates on reserves and on CBDC. That welfare gain requires a more countercyclical Taylor rule, which on its own yields a welfare gain of 0.57%, and a countercyclical CBDC interest rate rule with a response to a credit gap, which yields an additional 0.44%. Figure 3 shows the welfare consequences of different parameterizations of these two rules, with welfare gains from a higher inflation gap coefficient in the Taylor rule shown in the north-easterly direction, and welfare gains from a higher credit gap coefficient in the CBDC rule shown in the north-westerly direction.3

We also evaluate a number of alternatives to the rule behind Figure 3. They include CBDC quantity rules, a response to an inflation gap, rules for a CBDC model that merges wholesale reserves with retail money, and cash-like zero-interest CBDC. All of them, and especially a cash-like zero-interest CBDC, perform significantly worse. One alternative, a CBDC interest rate rule responding to a credit gap combined with countercyclical fiscal deficits, does significantly better. This is because these deficits are optimally financed almost exclusively with additional CBDC, and therefore represent a manifestation of the Friedman (1948) proposal of money-financed fiscal deficits.

Figure 3: Welfare Gains From Different Policy Rule Parametrizations

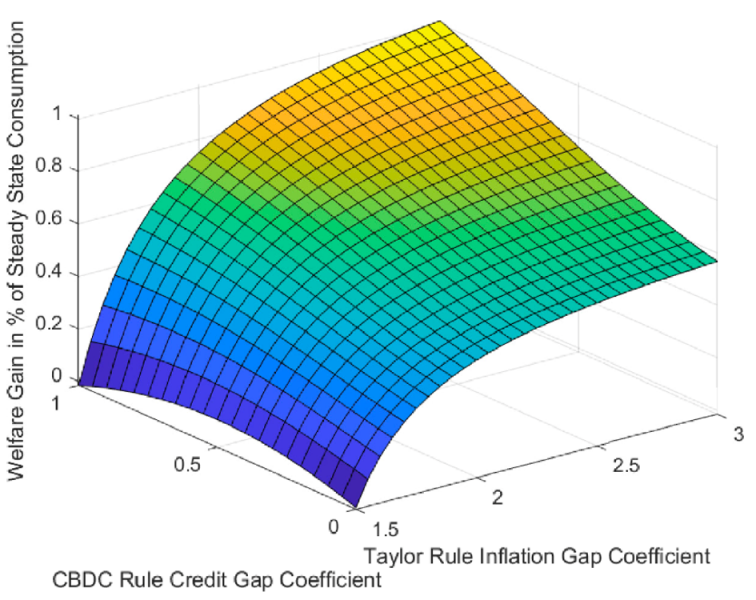
The reason for the superiority of credit gaps over inflation gaps is the important role of persistent financial shocks in both financial and real fluctuations, while inflation is much less persistent. The reason for the superiority of interest rate rules over quantity rules is that they allow non-banks to adjust their CBDC holdings more flexibly in response to financial shocks.

Finally, optimal policy calls for a smaller steady state spread between the two interest rates than in our baseline, in other words for a higher CBDC interest rate that implies a higher quantity of CBDC. Specifically, CBDC optimally equals around 40% of annual GDP.

What Might Have Been

Figure 4 compares the time series of the observed data (blue) to two counterfactual simulations, "Optimal without CBDC" (red) and "Optimal with CBDC" (black), that use the estimated shock series, but that replace the estimated Taylor rule of the pre-CBDC economy with optimized Taylor rules, and in the second case also an optimized CBDC interest rate rule. Both counterfactuals achieve a very significant smoothing of real variables. However, the pre-CBDC counterfactual does so around a far inferior steady state, and at the cost of substantially higher policy rate volatility. Furthermore, CBDC policies are much more effective at smoothing financial variables, as discussed in the next section.

Figure 4: Counterfactual Simulation for Optimized Simple Rules

Open Economy

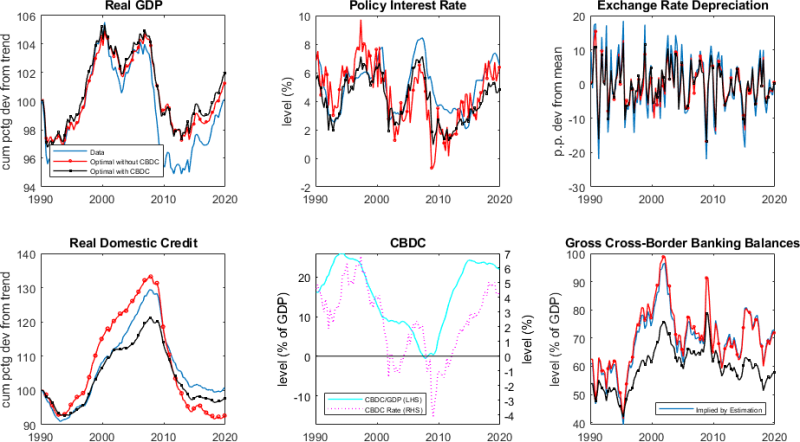
We find that optimized CBDC policies achieve reductions of around one third in the volatilities of cross-border (and also domestic) loan and deposit balances and of the exchange rate. Global runs into CBDC, under the central bank convertibility rules we propose, would not be runs from bank deposits, but runs from government bonds. Such shocks, even if extremely large, can be flexibly accommodated with small real effects, especially when CBDC is supplied flexibly subject to an interest rate rule.

Summary of Policy Implications

The introduction of CBDC can produce very significant macroeconomic efficiency and stability gains, both domestically and in the open economy. The key to maximizing those gains is a well-designed CBDC policy. Our analysis delivers a set of important insights in that respect, which we summarize as follows:

1. CBDC is highly beneficial for steady state efficiency.
2. CBDC is highly beneficial for macroeconomic and financial stability.
3. Banks have little reason to worry about CBDC-driven disintermediation.
4. In a recession, all else equal, a higher rather than a lower CBDC rate is expansionary.
5. Traditional policy rules do not need to be as aggressive when countercyclical CBDC rules are used.
6. CBDC interest rate rules are preferable to CBDC quantity rules.
7. A CBDC rule should respond to credit gaps rather than inflation gaps.
8. A cash-like zero interest CBDC achieves inferior results.
9. A single CBDC used both as reserves and for retail transactions achieves inferior results.
10. Unconditional CBDC issuance exclusively against eligible securities, plus countercyclical CBDC policy rules, permits a flexible accommodation of financial shocks with minimal real effects.
    
    

References

Friedman, M. (1948). A monetary and fiscal framework for economic stability. American Economic Review 38 (3), 245—264.

Friedman, M. (1969), The optimum quantity of money, Macmillan.

Kumhof, M. and C. Noone (2021). Central bank digital currencies - design principles for financial stability. Economic Analysis and Policy 71, 553—572.