

The views presented in this paper are those of the authors alone and do not necessarily reflect those of the European Central Bank.
We empirically explore the relationship between house prices and interest rates. Asset-pricing theory suggests that real house prices respond to changes in real interest rates in a non-linear fashion. This non-linearity should be especially pronounced at very low real interest rates. Most existing empirical studies estimate models with a constant semi-elasticity, thereby ruling out by design the potential non-linearities between house prices and interest rates. To address this issue, we estimate a panel model for the euro area countries with a constant interest rate elasticity (as opposed to a constant semi-elasticity), which is consistent with asset pricing theory. Our empirical results suggest that, in a low interest rate environment such as the period between 2015 and 2021, non-linearities in the house price response to interest rate changes are important: an increase of real interest rates from ultra-low levels could lead to downward pressure on real house prices three to eight times higher than the literature suggests.
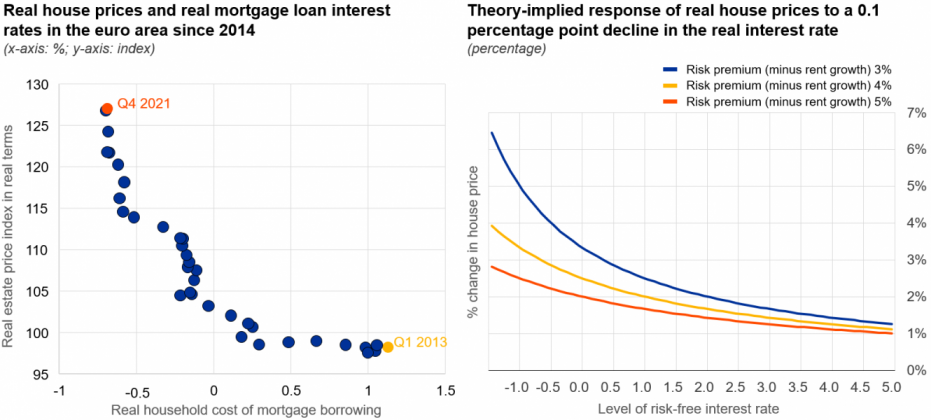
The acceleration of house price growth amidst falling interest rates to record-low levels across euro area countries between 2015 and 2021 has sparked renewed interest in the link between the two variables. Annual euro area residential real estate (RRE) price growth reached 9.5% in Q4 2021—the highest growth rate observed then for over 20 years—while in half of the euro area countries RRE price growth surpassed 10%. At the same time, interest rates on mortgage loans reached a historic low during 2021 of 1.3% in nominal terms. The extent to which changes in interest rates are associated with changes in house prices is foremost an empirical question and measured by the interest rate elasticity of house prices. However, empirical estimates of the interest rate elasticity of house prices vary significantly in the literature (Iossifov, Čihák and Shanghavi, 2008; Adelino, Schoar and Severino, 2012). Importantly, most studies presented above speak of elasticities, while, in fact, they are estimating semi-elasticities (common in log-linear model settings), i.e. percentage changes in house prices in relation to percentage point changes in interest rates. On average, a value for the semi-elasticity of around -3 is reported. This number implies that real house prices should drop by 3% if real interest rates rise by 1 percentage point. At the juncture of rising inflation and monetary policy reversal, elasticity estimates taking into account the specificities of a preceding ultra-low real interest rate environment are crucial for gauging the potential for house price corrections.
With few exceptions (Himmelberg, Mayer and Sinai, 2005; Kuttner, 2012; Lim and Tsiaplias, 2016; Igan, Kohlscheen and Rungcharoenkitkul, 2022), previous estimates of how house prices respond to interest rates have frequently ignored the fact that asset pricing theory implies a non-linear relationship between the two. Looking at the euro area aggregate, there indeed seems to be a strong negative (possibly non-linear) relationship between real mortgage loan interest rates and real house prices (Figure 1, left). In our analysis,1 we provide a simple empirical model of house price determination that is able to capture meaningful non-linearities between real house prices and real interest rates and, thus, helps to improve policy makers’ ability to gauge the impact of a policy-induced reversal of the (long-term) real interest rate. We also show that these non-linearities are a direct implication from asset-pricing theory.
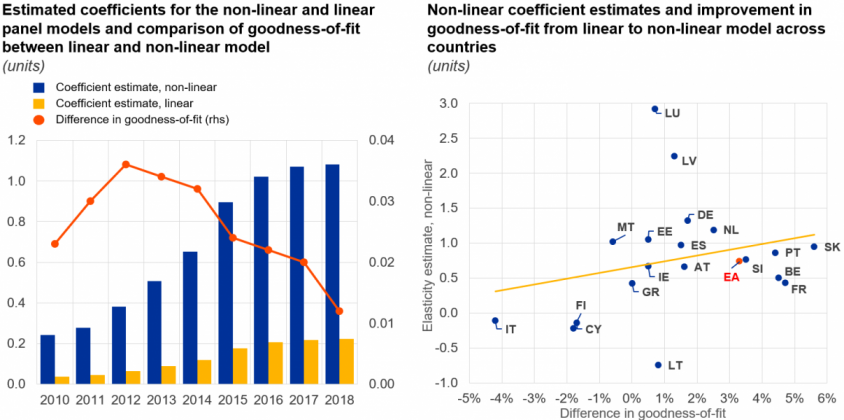
Notes: A positive difference in goodness-of-fit indicates that the non-linear model outperforms the linear model and vice versa.
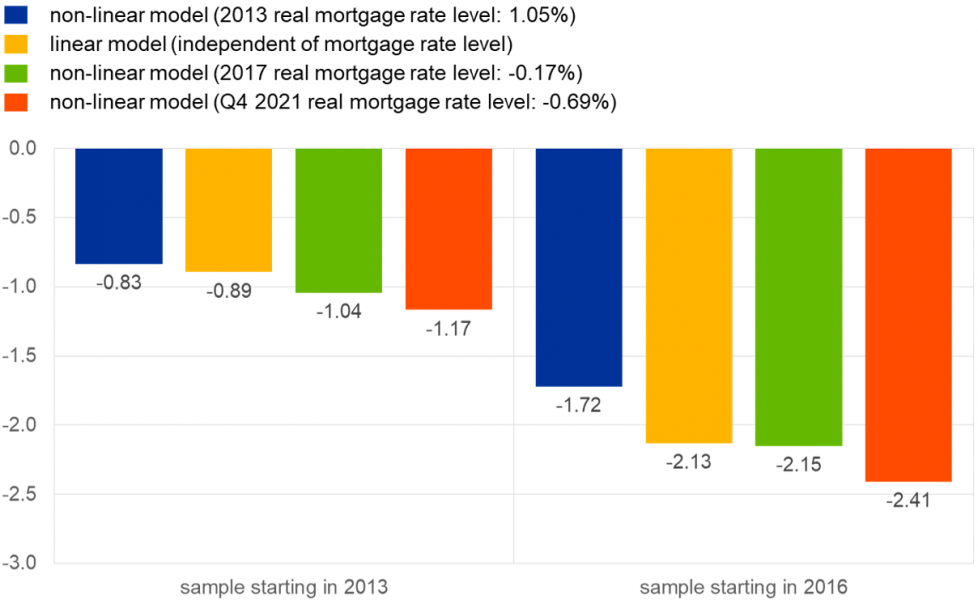
In summary, based on the panel elasticity estimates above and the Q4 2021-level of real interest rates, an increase in real interest rates by just 0.1 percentage points within one quarter could lead to downward pressure on real house prices of between -2.4% and -1.2% across euro area countries, depending on which estimation start date is chosen to obtain the elasticity estimates. Compared to the literature’s average semi-elasticity estimate of -3, which implies a -0.3% change in house prices for a 0.1pp increase in the real interest rate, we retrieve a house prices response that is four to eight-fold as strong in an environment of very low real interest rates. When compared to the linear model on the same estimation sample, the difference (i.e., between the red and yellow bars in Figure 3 above) in the impact on real house prices of a 0.1pp change in the real interest rate comes out to 28 basis points at the end of the sample.
Lim, G. C., & Tsiaplias, S. (2016). Non-linearities in the relationship between house prices and interest rates: Implications for monetary policy. Melbourne Institute Working Paper Series, No. 2/16. University of Melbourne.
This analysis is based on Dieckelmann et al. (2023) to which the interested reader may refer for further details on data, methodology and robustness.