

Contagion during times of financial stress is a complex phenomenon underlying systemic risk. In a recent paper we study one possible channel of contagion- the ‘credit quality channel’- and model related losses under assumptions of non-linearity in shock transmission and heterogeneous expectations in agents’ assessment of their counterparties due to uncertainty over future outcomes. We simulate multiple possible outcomes using granular data on the Spanish interbank market and find that: a) non-linear contagion leads to substantially larger losses than its linear counterpart for a wide range of intermediate levels of stress in the system, while its effects become negligible for very low and very high stress levels and b) incorporating uncertainty also increases estimated losses, yet the effect is smaller than that of non-linear contagion and most important around levels of stress which render parts of the system unstable.
Since the beginning of the 2000s a growing body of literature has focused on understanding the propagation and amplification of shocks through networks of financial interlinkages so as to identify structural features in these networks that can lead to systemic risk (Bougheas and Kirman, 2015; Glasserman and Young, 2016; Caccioli et al., 2018; Jackson and Pernoud, 2021). This type of analysis allows to capture second-round effects, which refer to interactions between entities not necessarily directly connected, which are elusive when studying the system as a collection of independent entities or disconnected bilateral contracts.
In our recent analysis we focus on the interbank market, an essential component of modern financial systems. These markets are important for the liquidity management of credit institutions, risk sharing and the transmission of monetary policy. Shocks can spread rapidly in the interbank market through multiple channels. For instance, creditors can suffer losses if borrowers are unable to meet their contractual obligations, liquidity shortages can occur because of a loss of confidence in certain borrowers and valuation losses are generated when banks write down interbank assets due to a perceived worsening of the credit quality of their counterparts. The latter constitutes the so-called credit quality channel (Battiston et al., 2012; Fink et al., 2016; Barucca et al., 2020) and is the main focus of this paper.
The credit quality channel operates when a negative shock to the equity of a bank leads to its creditors increasing their estimates of this borrower’s probability of default. As a consequence, the value of the corresponding interbank claim they hold is reassessed downward. The extent of the reassessment depends on creditors’ perception regarding the deterioration of the borrower’s balance sheet (before the materialisation of an actual default).
Using data from the Spanish Credit Register1, we study potential contagion losses via the credit quality channel in the Spanish domestic interbank market. We build on the popular framework by Battiston et al. (2012), which has come to be known as DebtRank and is widely used in empirical applications. In this framework, creditors are assumed to react linearly when the value of the equity of their borrowers decreases and these reactions are assumed to be independent of the initial balance sheet structure of the borrower. We argue, however, that the size of the losses experienced by the borrower significantly affects the reaction of the corresponding creditors as does the initial capitalisation of the borrower. Poorly capitalised borrowers experiencing even small equity losses lead to strong creditor reactions while better capitalised entities are able to withstand larger losses before triggering any significant reaction. We also argue that creditors’ assessments of the probability of default of their borrowers are heterogeneous and surrounded by uncertainty since there is no generally accepted method for estimating whether a counterparty will default within a given time horizon.
We, thus, consider creditors take into account both equity losses and the leverage ratio of the debtors when assessing their probability of default and do so in a non-linear manner as explained above. We also explicitly model uncertainty by adding a stochastic component to these otherwise deterministic assessments2. We introduce these assumptions in the DebtRank framework and explore whether total losses (the sum of estimated losses for all banks in the network) are amplified or dampened with respect to the results obtained with the linear and deterministic DebtRank model.
When exploring the effects of these assumptions on the dynamics of contagion, we are interested not only in their impact under current market conditions, but also across different stress scenarios the system could be subject to. We therefore consider a wide range of hypothetical situations characterised by different system leverage ratios, from a situation of severe capital scarcity in the system (∼ 0.1%) to one of capital abundance (∼ 99%), always with respect to total assets in the system.
In order to study the propagation of financial distress across the network of financial institutions, an initial shock must be introduced in the system. Following most of the literature on distress propagation before default (Caccioli et al., 2018), we introduce the initial shock as a relative devaluation of a bank’s external assets (i.e. non-interbank assets). It is this devaluation that leads to a proportional equity loss for the bank in question. The results presented here correspond to an initial shock of a 0.5% devaluation of external assets.
We run as many simulations as banks there are in the network using both DebtRank and our modified framework and compare results at the system level. We first incorporate separately the non-linear and uncertainty component and then combine the two components. When considering the extension of the model with uncertainty, results are further averaged over 1.000 different realisations of the stochastic component.
The impact of the non-linear component is very relevant as it drives losses up within a wide range of system-wide stress levels around the centre of the studied spectrum. This can be clearly observed for leverage ratios between 0.8% and 8%, with losses derived from the non-linear model being about 13 times larger than losses obtained with DebtRank. With a system-wide leverage ratio below 0.8% or above 8%, losses become very similar between both models since the system is either highly stressed and prone to amplification or highly stable.
Figure 1 illustrates this comparison, with the vertical axis representing the total system mean loss corresponding to each of the two models and the horizontal axis covering the broad range of system-wide leverage ratios studied, from slightly below 0.1% to slightly above 99%. The area where non-linear contagion has a strong effect on the results is just below current market conditions (marked with a dotted black vertical line). In other words, even a small deterioration of leverage ratios would suffice to make non-linear contagion crucial in accounting for potential losses via the credit quality channel.
Figure 1: Linear vs nonlinear contagion
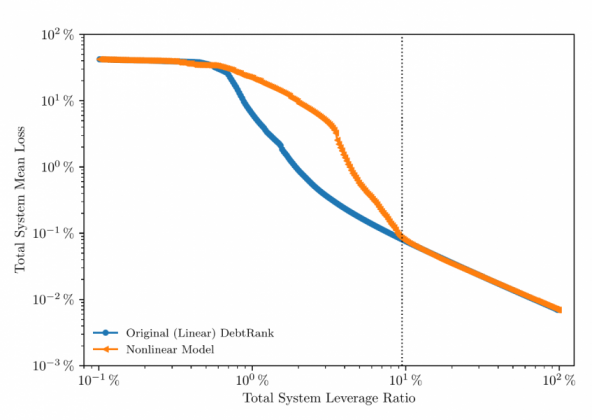
Note: The chart shows the effect of non-linear contagion by comparing total system mean loss for both the non-linear model (orange) and the original (linear) DebtRank model (blue). Only the losses caused by the propagation of the shock through the network is shown. The dotted black vertical line marks the actual leverage ratio of the system in our data.
We find that under current market conditions, uncertainty seems to have, on average, a negligible impact on the results. More broadly, uncertainty seems to have a mostly negligible effect, on average, when the banking system is either under very low levels of stress (high leverage ratios) or under very high levels of stress (low leverage ratios). However, for intermediate levels of stress (intermediate leverage ratios) the average results of both models diverge significantly, with important fluctuations in the sign of these differences, from negative values around 9% to positive values around 5%. Figure 2 illustrates the comparison, with the vertical axis representing the total system mean loss corresponding to the model with uncertainty relative to the original (deterministic) DebtRank model. Values above (below) 100% imply an increase (decrease) in losses due to uncertainty. On the horizontal axis, we present results for the same range of system-wide leverage ratios as in Figure 1. When we move away from average results and focus on the 5 – 95 percentile range (grey shadow in Figure 2), we see losses more than triple with respect to the average result.
Figure 2: Deterministic model vs model with uncertainty
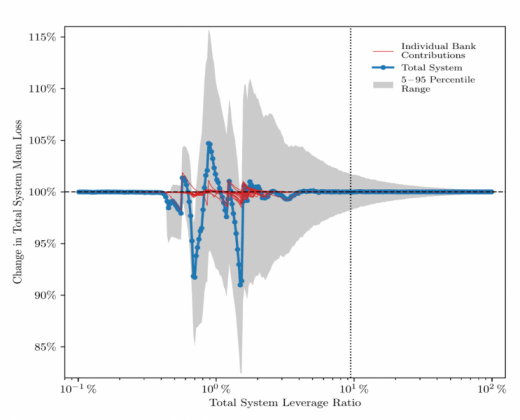
Note: The blue line represents the change in total system mean loss, that is, the total system mean loss of the model with uncertainty relative to the original (deterministic) DebtRank case. The grey shadow indicates the 5 – 95 percentile range for this variable. The red lines show the contribution of each bank to this change, i.e. the blue line is a weighted sum of the red lines. The dashed black horizontal line marks the line of equality, when both models lead to the same results. The dotted black vertical line marks the actual leverage ratio of the system in our data.
When comparing the results of both components in our framework with those of the original DebtRank model (linear and deterministic), the difference in total system mean losses is fundamentally driven by the non-linearity and the relation between the two frameworks would look remarkably similar to that shown in Figure 1. However, in this case, the leverage ratio at which uncertainty starts being important —when moving from higher to lower values of system leverage ratios— is much higher in the non-linear case, and thus much closer to current market conditions. In particular, the leverage ratio at which uncertainty starts having a strong impact moves from roughly 1.5% in the linear case presented in Figure 2 to approximately 5% in the non-linear case. The magnitude of the change in average losses produced by the inclusion of uncertainty is also larger in the non-linear case, where this change moves between −14% and +6%.
When assessing contagion in financial networks, the assumptions regarding agents’ behaviour are relevant for gauging potential losses. The agents we have studied are banks and they develop exposures to each other in the interbank market, which can be treated as a network of interconnected nodes, where interconnectedness materialises through bilateral lending contracts. Contagion can occur when shocks to one bank’s balance sheet affect other banks due to their exposures to the former and, therefore, initial losses are amplified. We find it is particularly important to take into account that transmission can be non-linear, i.e. that highly leveraged banks are perceived by their counterparties as having a higher probability of default than less leveraged banks experiencing shocks of the same magnitude. At the same time, we find it is also relevant to account for uncertainty in the assessments banks make of one another’s solvency since this can lead to considerable differences with respect to deterministic assessments. These results are conditional on the level of stress in the system, which we proxy by the level of total leverage in the system.
While we have focused here on the credit quality channel, we expect our findings to be relevant also for other contagion channels, particularly for those where creditor assessments of counterparty default risk play a role, such as short-term liquidity withdrawal triggered by a loss of confidence in the counterparty.
Battiston, S., M. Puliga, R. Kaushik, P. Tasca and G. Caldarelli (2012). “Debtrank: Too central to fail? Financial networks, the fed and systemic risk”, Scientific Reports, 2, p. 541.
Bougheas, S., and A. Kirman (2015). “Complex financial networks and systemic risk: A review”, in P. Commendatore, S. Kayam and I. Kubin (Eds.), Complexity and Geographical Economics: Topics and Tools, Springer International Publishing, pp. 115-139.
Caccioli, F., P. Barucca and T. Kobayashi (2018). “Network models of financial systemic risk: a review”, Journal of Computational Social Science, 1, pp. 81-114.
Carro, A., and P. Stupariu (2022). Uncertainty, non-linear contagion and the credit quality channel: an application to the Spanish interbank market, Working Paper, Banco de España.
Glasserman, P., and H. P. Young (2016). “Contagion in financial networks”, Journal of Economic Literature, 54(3), pp. 779-831.
Jackson, M. O., and A. Pernoud (2021). “Systemic risk in financial networks: A survey”, Annual Review of Economics, 13(1), pp. 171-202.
A granular database managed by the Banco de España with abundant information on credit exposures of institutions operating in Spain. For more information, visit: https://www.bde.es/bde/en/areas/cenbal/ .
For more details on the methodology and the underlying behavioural assumptions, please see Carro et al. (2022).