

1. Introduction
Since 2014, a large share of banks’ net operating income in the euro area arises from non-interest income activities where net fee and commission income (NFCI) and net trading income (NTI) are the most important contributors. Diversification of income sources can have unintended consequences; it can create new risks and challenges for the banking sector. From a regulatory perspective, quantifying these balance sheet items’ evolution in a stress scenario remains a relevant and unmet need. Modelling non-interest related sources for stress-test purposes is not straightforward as the source of risks and the channel of transmission might differ from the one already investigated in the literature. For instance, trading income is likely to be much more volatile and responsive to financial developments while credit risk is related to slow moving macro variables.
We empirically estimate the linkages between financial risk factors and net trading income. We focus on net trading income as it is the most volatile and riskiest of all the non-interest income activities. The set of macro-financial risk factors in our methodology is restricted to those provided in previous EU-wide Stress Test scenarios. We select the main risk factors that are linked to various types of financial assets according to the underlying securities broken down in the following risk categories: interest rate products (fixed income securities and interest rate derivatives), credit products such as credit swaps, equity products and commodity related products. Therefore, we select a few risk factors for each category to summarize the possible risk drivers for the different financial assets. To estimate the distribution of NTI conditional to changes in key macro-financial risk factors we implement a fixed effects quantile dynamic regression model. We estimate the model semi-parametrically using the method of moments technique proposed by Machado and Silva (2019). Our sample includes 54 European banks from 13 countries that participate in the EU-wide Stress Test and that are directly supervised by the SSM.
2. Results
We estimate conditional quantiles using the method of moments for all quantiles ranging from 10th to 90th percentiles with 10 percentage point increments. We find a strong and asymmetric impact of the risk factors on the tails of the distribution of NTI over total assets (NTI/TA). In particular, long term interest rates, credit spreads and oil returns exhibit a strong positive effect on the lower quantiles of the NTI/TA distribution, an effect that dissipates over higher quantiles. On the other hand, stock returns have a significant (positive) effect only on the right tail of the NTI/TA distribution. We also find that bank specific characteristics such as the amount of risk weighted assets and the total equity the bank holds are poor indicators of NTI/TA performance across quantiles.
The volatile nature of trading income can lead to increased downside tail risk, that is, the risk that a bank experiences an extreme trading loss. Extreme returns cause “fatter” tails than a normal distribution would predict. Inter-linkages between financial risk factors and trading income indicate that financial crisis and adverse market shocks can produce left tail events which could have a damaging impact on the trading portfolio. Following Adrian, Boyarchenko and Giannone (2019) we map the estimates of the quantile function into a probability density function. From this we gauge the (time-varying) conditional expected shortfall of CET1 ratio1 due to changes in NTI at different time horizons and across banks. Figure 1 shows the smoothed conditional distribution functions for two selected periods: the last quarter of 2019 and the first quarter of 2020. The conditional distribution is very sensitive to changes in financial risk factors. During the onset of the Covid-19 pandemic the tails of the distribution have become fatter, especially the left tails for many of the 54 selected banks. The visible shift to the left and fattening of the tails implies that there is a higher probability of the bank experiencing both negative and extreme NTI losses in following quarter.
Figure 1: Conditional distribution NTI/RWA Q4 2019 and Q1 2020
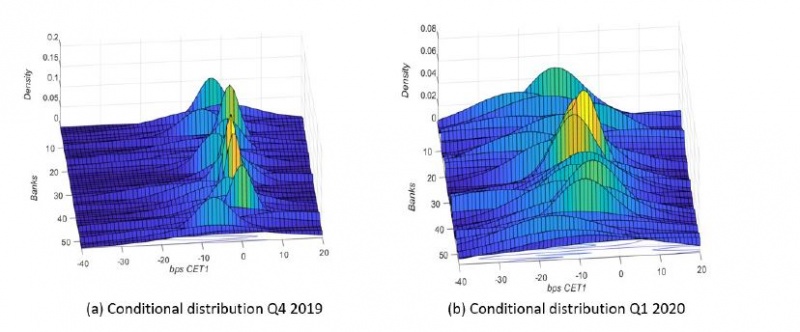
Note: The panels show the estimated conditional smoothed distribution for NTI/RWA. The left panel shows the conditional distribution in Q4 2019, and the right panel in Q1 2020. Each bank in the sample is represented along the z-axis. NTI has been restated relative to risk weighted assets (RWA) so as to measure the expected impact on the bank CET1 ratio. NTI/RWA is presented in basis points.
Using expected capital shortfall, we can quantify the tail risk as the expected loss conditional on the bank experiencing an extreme event (a loss greater than the 5th or 10th percentile for example). We find that at the onset of the Covid-19 pandemic the expected CET1 ratio shortfall due to trading income losses at the 5th percentile ranges between approximately -20 and -150 basis points, reaching the lowest level in the forecasted horizon (see Figure 2).
Figure 2: Expected shortfall (5th percentile) – Full sample
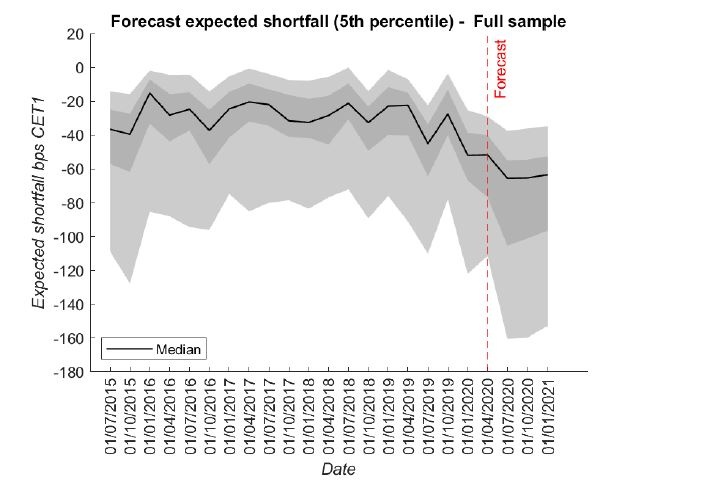
Note: The graph shows the 5th percentile expected shortfall for banks over the period 2015 – 2020 Q1, including the forecasted 4 quarters ahead (Q2 2020 – Q1 2021). Each quarterly observation on the graph shows the cross-sectional distribution across the sample of banks. The black line represents the bank with the median expected shortfall, the shaded dark grey defines the banks at the 30th to 70th quantiles and the lighter grey the 10th and 90th quantiles. Expected shortfall is expressed in basis points of NTI/RWA.
One of the objectives of stress-test models is to forecast banks’ balance-sheet items under different hypothetical stress scenarios. The severity of the stress scenarios is directly related to the realizations of the market risk factors. In this respect, our stress scenarios can be calibrated to the respective quantiles of the risk factors giving a clear and intuitive interpretation of the scenario and the implied loss distribution. We use the model to deliver multi-step forecasts of NTI/TA and NTI/RWA for various quantiles that reflects different degrees of scenario severity.
3. Conclusions
We show empirically the heterogeneous and asymmetric impact of financial risk factors on the distribution of NTI/TA across a large sample European Banks. We estimate via the method of moments a dynamic fixed effects quantile model and we demonstrate how it can be used to derive plausible measures and probabilities of a capital shortfall for stress test participating banks. The model can be used for stress test exercises. The values of financial risk factors are available in real time from various market providers. Using the model it is possible to project the NTI taking into account the possible development of macro-financial variables and banks’ characteristics. Our methodology could be also employed and extended in other non-interest income sources such as commission fees and operation income. The key risk factors are likely to differ, but distributional effects should also be substantial. With the exemption of Coffinet, Lin, and Martin (2009) and Kok, Mirza and Pancaro (2019) the literature on other sources of income is scarce.
Adrian, Tobias, Nina Boyarchenko, and Domenico Giannone (2019). “Vulnerable Growth”. American Economic Review, 109(4), pp. 1263–89
Coffinet, Jérome, Surong Lin, and Clément Martin (2009). “Stress testing French banks’ income subcomponents”. Banque de France Working Paper.
Kok, Christoffer, Harun Mirza, and Cosimo Pancaro (2019). “Macro stress testing euro area banks’ fees and commissions”. Journal of International Financial Markets, Institutions and Money, 61, pp. 97–119
Machado, José AF and JMC Santos Silva (2019). “Quantiles via moments”. Journal of Econometrics, 213(1), pp. 145–173
CET1 ratio is computed as Common Equity Tier 1 Capital over Risk Weighted Assets.