

This policy brief summarises the key findings in Altermatt,L., van Buggenum H., Voellmy L. (2022), Systemic bank runs without aggregate risk: how a misallocation of liquidity may trigger a solvency crisis, SNB Working Paper no. 10/2022. The views expressed in this policy brief are those of the authors and do not necessarily reflect those of the Swiss National Bank.
Systemic bank runs have long been an important topic in macro-financial economic research and the financial crisis of 2007-09 has only highlighted their importance further. Empirical observations show that systemic runs usually occur simultaneously with downturns in economic activity. While a recession might increase the probability of a bank run, we argue that causality may also go the other way: a systemic bank run impairs the use of bank deposits to settle transactions, which hinders economic activity and causes the downturn. In our paper, we propose a model that captures this mechanism and discuss possible remedies. A key insight is that interventions which restrict deposit withdrawals in a run can be self-defeating due to their negative effect on demand in goods markets.
Douglas Diamond and Philip Dybvig were recently awarded the Nobel Memorial Prize in Economics, in large part for their seminal work on banking instability in Diamond and Dybvig (1983). Diamond and Dybvig’s model shows how bank runs can cause fundamentally sound banks to collapse. One key result in their paper is that runs can be prevented if banks commit to freeze deposits after a certain number of withdrawals. By imposing a freeze, banks prevent liquidation of their long-term investments at a loss and thus ensure their solvency. In our paper, we highlight an important caveat to this line of reasoning. Given the role that deposits play in settling transactions, a deposit freeze may create an economic downturn by limiting households’ capability to spend on consumption. Rather than bolstering banks’ solvency, a freeze might therefore exacerbate losses on bank assets.
The main innovation in our paper is the way in which the banking system’s assets and liabilities are connected. Banks issue loans to entrepreneurs who sell goods to households, which in turn pay for the goods by redeeming bank deposits. The return on bank assets, i.e., loans to entrepreneurs, is thus contingent on households being able to withdraw their deposits. As is standard in bank run models, only some of the households have consumption needs (impatient depositors), whereas others do not want to consume (patient depositors). In a run, some impatient depositors fail to withdraw, since part of banks’ cash reserves end up in the hands of patient depositors, who just save the cash. This lowers revenues of entrepreneurs, which causes some of them to default on their loans obtained from banks. The anticipation of these defaults makes it optimal for patient depositors to run the banks if others do so too. If banks react to a run by imposing a freeze, this may further depress demand in goods markets and increase loan defaults, thus exacerbating rather than relieving the situation.
Incorporating the role of bank deposits in settling economic transactions overturns the canonical result that a full deposit freeze prevents belief-driven runs when there are no fundamental shocks. At the same time, a `laissez-faire’ policy under which banks pay out depositors until their cash reserves are depleted, is no remedy against runs either. In order to prevent runs, banks therefore need to put some limits on withdrawals once redemptions exceed a certain level, while still allowing for sufficient withdrawals to keep economic activity going.
We show that under some conditions, banks can prevent runs by imposing properly calibrated redemption fees combined with partial freezes. In order to eliminate runs, such a policy needs to satisfy three criteria: (i) it must be suboptimal for depositors without consumption needs to withdraw once the policy is implemented; (ii) it must be optimal for depositors with consumption needs to continue withdrawing once the policy is implemented; (iii) given that the run is stopped once the policy is implemented, it must be suboptimal for depositors without consumption needs to run in the first place.
Whether there exists a suitable combination of redemption penalties and partial deposit freezes that eliminates runs depends on the model’s parameters. The larger the loss-absorbing buffer banks have in normal times, and the earlier banks can react to runs, the more likely it is that runs can be prevented with these measures.
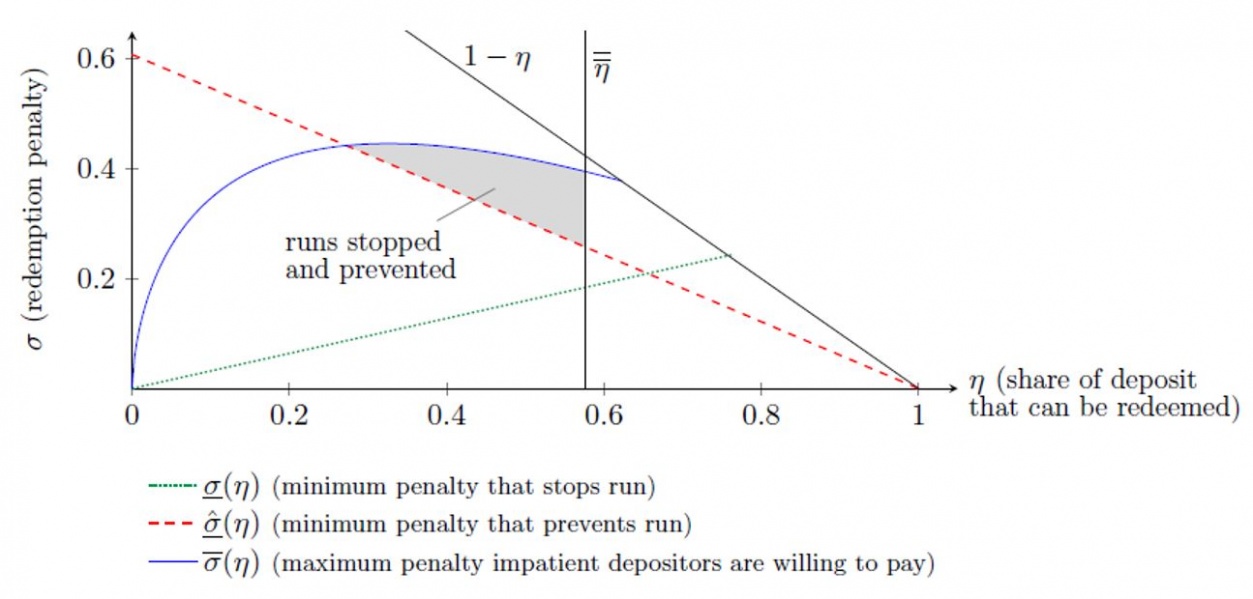
Properly calibrating the response to a run can be challenging. As an example, Figure 1 shows the combinations of redemption penalties and partial freezes that can both stop a run once it has started and prevent the run from starting in the first place, for a given parametrization of the model. One the one hand, the redemption penalty should be high enough to deter depositors without consumption needs from withdrawing once the penalty is imposed (green line). On the other hand, the penalty should be such that depositors with consumption needs still find it optimal to withdraw (blue line). Next, and more subtly, in order to deter depositors from running before penalties or freezes are imposed, the revenue collected through redemption penalties in a hypothetical run scenario must be large enough (red line). Finally, the amount that can be paid out is limited by banks’ cash reserve (black vertical line). Of course, the position and slope of the different lines will depend on the parametrization, and a policy that satisfies all criteria may not exist.
Figure 1: Combination of redemption penalties and partial freezes that eliminate runs
Our set-up starts from the premise that, in normal times, households withdraw cash from banks in order to purchase goods. A run depresses economic activity by limiting households’ access to cash. The model is thus particularly relevant for cash-intensive economies, i.e., developing economies today, or historical episodes in the U.S. and Western Europe. We also believe that our model may apply to situations where physical cash is not involved, for example, the run on shadow banks in the financial crisis of 2007-2009 or runs on banks in small-open economies, such as in Cyprus in 2012-2013. As long as a run hinders access to liquid assets by agents who would like to consume, our mechanism applies.
While it seems plausible that our mechanism is at play to some extent in many bank run episodes, we want to highlight one where it may have been particularly important, namely the deposit freeze in Argentina in 2001-2002. The freeze was enacted in late 2001 in order to stop a bank run, and it restricted cash withdrawals from banks. Since the Argentinian economy was relatively cash-intensive at the time, the restricted access to cash had negative effects on economic activity and contributed to a sharp drop in GDP. Even with the deposit freeze in place, pressure on banks did not stop. While we do not want to claim that this episode was solely caused by belief-driven bank runs, it seems likely that the crisis was amplified by what we model, as it features all the relevant aspects of our mechanism.
So far, we have focused on run-preventing measures that banks can take without a public safety net. In our paper, we also study emergency liquidity provided by a central bank that buys illiquid assets from banks in case of a run. Injecting emergency liquidity can always stop runs once they have started. It can also prevent runs from starting in the first place, but only if the central bank purchases assets at or close to face value. Doing so ensures that banks can continue paying out the promised amount to depositors with consumption needs, which stabilises aggregate demand.
In a sense, our result goes against Bagehot (1873), who advocated for central banks to lend to illiquid yet solvent banks at a high rate of interest. While Bagehot’s policy prescription seems natural, furnishing enough cash to households (through banks) is key in order to maintain economic activity in our model. When the central bank charges a penalty rate on emergency liquidity, banks need to pass on the penalty to withdrawing depositors. As a result, depositors with consumption needs end up with less cash to spend, demand on goods markets is depressed, and entrepreneurs default on their loans. The banking system’s liquidity problem thus turns into a solvency problem if and only if the lender of last resort charges a sufficiently high penalty on emergency liquidity.
Bagehot, W. (1873). Lombard Street. Henry S. King & Co.
Diamond, D. W. and Dybvig, P. H. (1983). Bank runs, deposit insurance, and liquidity. Journal of Political Economy, 91(3):401–419