Regulators as Risk Managers: Macroprudential Policy through a Risk Management Lens

In a recent paper, we developed a set of modeling techniques through which we evaluate the size of macroprudential capital buffers across systemic banks in the Euro Area. We find sometimes substantial differences with the capital buffers currently assigned by national regulators. Since capital buffers are one of the main policy instruments for managing banks’ potential contributions to systemic distress, our findings have substantial implications for systemic risk in the EEA.

Regulators worldwide use macroprudential capital requirements as one of the key instruments to manage ex-ante the risks of a systemic crisis. Increasing the loss-absorbing capacity of large, economically important, interconnected banks reduces the chances of their default in adverse circumstances, and thus curtails the possibility that they can trigger cascading distress of related institutions.

However, there exists very little theoretically backed guidance on how to calibrate these macroprudential buffers. This not only makes it difficult to assess their adequacy in any given country but has also led to buffers of widely diverging stringency across countries within the Eurozone. For want of a generally accepted basic framework, aligning these diverging approaches has proven to be difficult (ESRB, 2017).

What makes things even more complex is that a large disconnect exists between the academic and regulatory approaches used to evaluate systemic risk. The academic approaches favor the use of market data and asset pricing methods (Huang et al., 2012; Brownlees and Engle, 2017; Adrian and Brunnermeier, 2016; Acharya et al., 2017). Regulators on the other hand rely on balance sheet and regulatory data to generate a score of systemic importance (EBA, 2020).

From Risk Measurement to Risk Management

In two recent papers, we address these gaps and discrepancies. In the process, we bring to light the role of a policymaker as a grand risk manager of sorts, balancing out the risks of a financial crisis when the banking sector is not well capitalized versus the risks of stifling lending and economic growth when capital requirements are raised too sharply.

First, in Dimitrov and van Wijnbergen (2023a), we develop а framework for measuring systemic risk and attributing it across a universe of European banks based on an approach used in the securitization industry to model the potential for loss in a portfolio of defaultable loans (Tarashev and Zhu, 2006). In that sense, the banking system is modeled as a portfolio of loans and systemic risk measures the potential loss for the sector given that multiple institutions default at the same time.

In Dimitrov and van Wijnbergen (2023b) we go a step further and determine the size of the macroprudential buffers that minimize the potential loss for the banking portfolio.

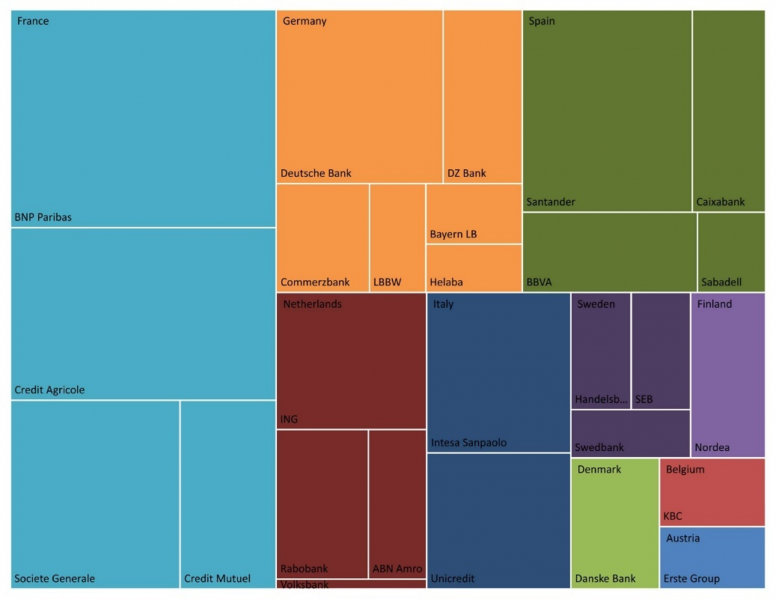
In both cases, we use market-driven estimates of systemic relevance. In contrast to the seminal approaches of Adrian-Brunnermeier’s CoVaR (Adrian and Brunnermeier, 2016) and Acharya’s MES (Acharya et al., 2017) which rely on co-dependencies in the tails of banks’ equity prices, we base our model on a credit risk model calibrated on the prices of single-name CDS contracts. This allows us to include in the analysis universe a number of banks whose equity is not publicly traded, either because they are privately held, cooperatives, or held by the government in some form. Figure 1 shows the full universe that we consider with the area of each rectangle indicating the liability size of each bank in the system.

Figure 1: Banks by Liability Size

CDS Prices

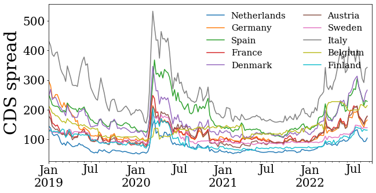
First of all, let us discuss briefly what a CDS contract is and why it carries important information on the fragility of the banking sector at a given point in time. In essence, it is an insurance contract, which is traded over-the-counter (OTC), and in which the protection buyer agrees to make regular payments, the CDS spread rate over a notional amount, to the protection seller. In return, the protection seller commits to compensate the buyer in case of default of the contractually referenced institution. There are multiple features of the contract that make it an attractive source of information on the risks which are evolving in the financial sector: the contract targets directly risks of insolvency, it has standardized terms and conditions, better liquidity than corporate debt, a tendency to lead equity markets in price discovery, and prices in government intervention and restructuring of the reference institution. Figure 2 shows the median bank CDS spreads per country in our sample and gives us an initial view of the common trends affecting creditworthiness between countries.

Figure 2: Median Bank CDS Rates per Country

Model Overview

There are several key mechanisms behind the method that we develop to optimally calibrate banks’ macroprudential capital buffers. First, we use a structured credit risk approach to relate the default risk of a single bank to its capital requirements. This follows from the observation of Merton (1974) that equity under limited liability is in fact a call option on the assets of the firm, as default occurs when the market value of the firm’s assets falls below the face value of its debt. Developing the argument a step further, we relate analytically the default probability to the ratio of common equity to debt that banks are required to hold. By requesting higher capital buffers, regulators make banks safer by forcing them to deleverage.

Second, as a measure of systemic risk exposure, we look at the propensity of multiple banks to default at the same time. We rely on a Vasicek-type factor model typically used for the estimation of the risk of a portfolio of loans. In this approach, a set of common factors across all banks drives the common variation in their creditworthiness. The individual exposure of banks to the market factor (or factors) will determine the degree to which their risk is driven by the market and the degree to which it is idiosyncratic. Time co-variation in the single-name CDS spreads of the underlying banks allows us to estimate these factor exposures.

Third, we develop two approaches to map the measure of systemic importance into add-on macroprudential buffers. The first one builds on the Equal Expected Impact (EEI) approach through which supervisors aim at equalizing the expected default loss between systemic institutions and a non-systemic reference bank (EBA, 2020). In this approach, regulators use the systemic score that each bank gets as a crude measure of its social Loss Given Default (sLGD). By managing banks’ probability of distress through setting buffer requirements, the expected losses of distress are equalized. In our rendition of the method, instead of using regulatory scores, what is equalized is the expected systemic cost between banks, which factors in the probability that other banks will become distressed given that one particular bank is in distress. The propensity for joint distress is measured through the CDS-implied default probabilities on banks’ subordinate debt.

Resulting Capital Buffers: Impact Equalization vs. Risk Minimization

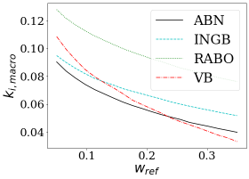
Figure 3 demonstrates that the resulting mapping from scores to buffers with the EEI approach depends strongly on the reference institution chosen and the weight this institution gets assigned. The larger the size of the reference bank that is considered non-systemic, the less conservative the policymaker will be in setting macro capital buffers to each of the systemic banks.

Figure 3: Macro Buffer with the EEI Approach (Dutch subsample)

In order to overcome the necessity of pinpointing a reference size and affecting capital buffers in that way, we also develop an alternative to the EEI. We formulate the capital calibration problem as an optimization problem. In the first step, macroprudential capital requirements are set for individual banks to minimize the potential tail loss of the system, subject to an average target ratio. In the second step, a policymaker weighs the social costs and benefits of higher buffers and picks the average capitalization rate that minimizes the corresponding social cost function.

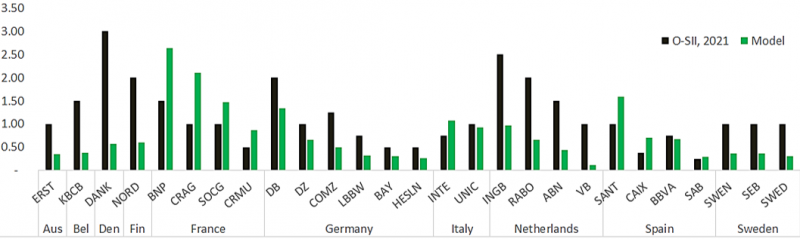
In Figure 4 we show the model-based rates if the macroprudential policy was set on a European scale and if a
policymaker targets the current average O-SII rates, assuming that it is socially optimal. The figure compares the model-based outcomes to the current national O-SII rates. The numbers represent the CET1 capital buffer add-on that banks need to maintain to stave off the risk they contribute to the system. Our model prefers to allocate consistently higher buffers to the large French and to some extent Spanish banks, while it compensates by allocating lower buffers to the Netherlands and Germany.

Figure 4: Optimal Macro Buffers at Current O-SII average

We then take this approach one step further. In the second, step we derive the target macro buffer rate. This can be done by balancing a trade-off: higher capital adequacy in the system indicates reduced expected costs of distress, but at the same time may lead to social loss if the stringent requirements stifle the credit supply to the economy. We balance the two, calibrating the trade-off based on recent empirical studies of the relationship between capital adequacy, credit, and economic growth.

Figure 5 then shows the distribution of the socially optimal total CET1 capital based on the model, compared to the corresponding capital. Once again, we obtain similar results, with some areas where banks seem undercapitalized relative to the model recommendation and others with apparent overcapitalization compared to the model optimum. The clearest outlier is France, where the model recommends higher capital ratios for all banks in the universe except Credit Mutuel (CRMU), a cooperative bank. The model output also indicates that Germany’s Deutsche Bank (DB), and Spain’s Santander (SANT) should have higher capital than they currently have. On the other hand, Dutch and Swedish banks appear with significantly higher capitalization ratios in practice than required by the model.

Figure 5: Fully model-based optimal capital ratio’s (%)

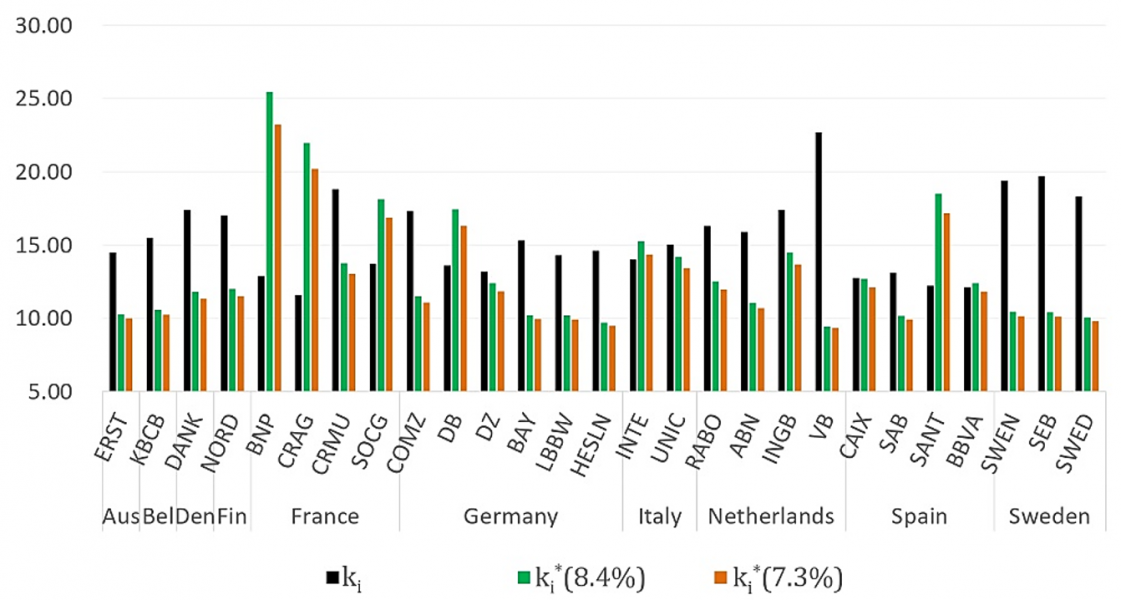
Interestingly, the two Italian banks in our sample – Intesa Sanpaolo (INTE) and Unicredit (UNIC) – do not show a significant difference between actual and model outcomes. Even though the median spread on the Italian banks in our sample appears to be the highest compared to that of other countries throughout the evaluation period (see Figure 2), the two banks are smaller on a European scale – as Figure 1 shows, they are less than half the size of BNP for example – which lowers the potential that they will dominate the system and thus lowers the need for larger buffer due to systemic concerns within Europe.