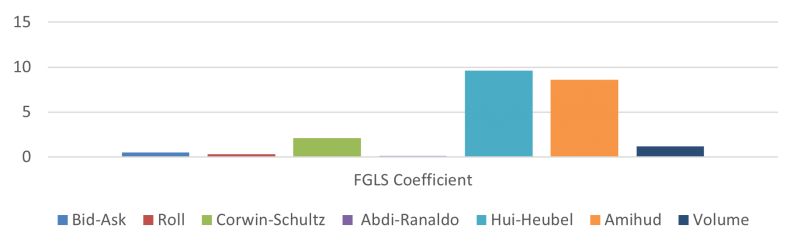
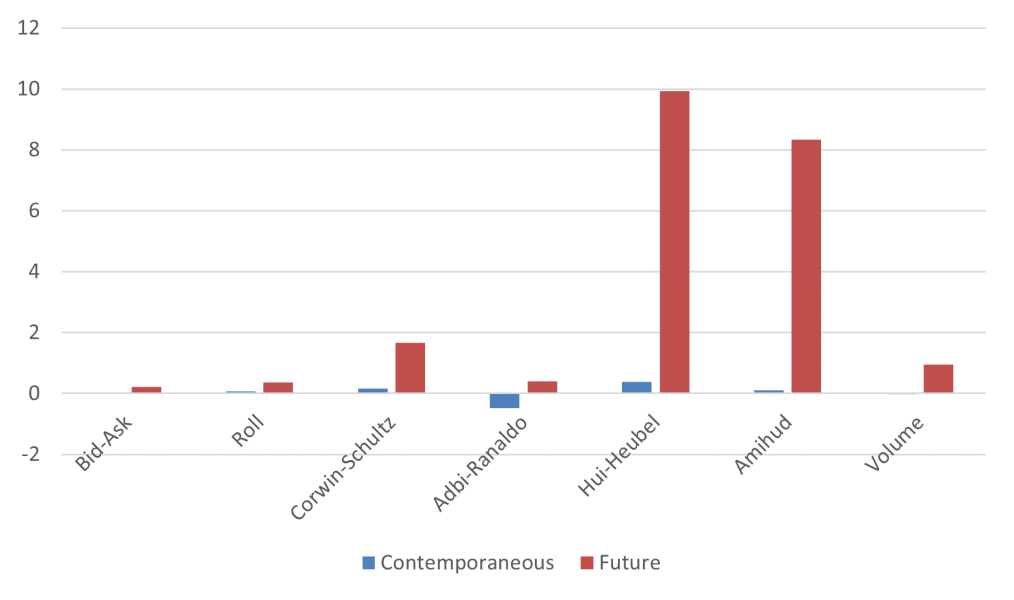
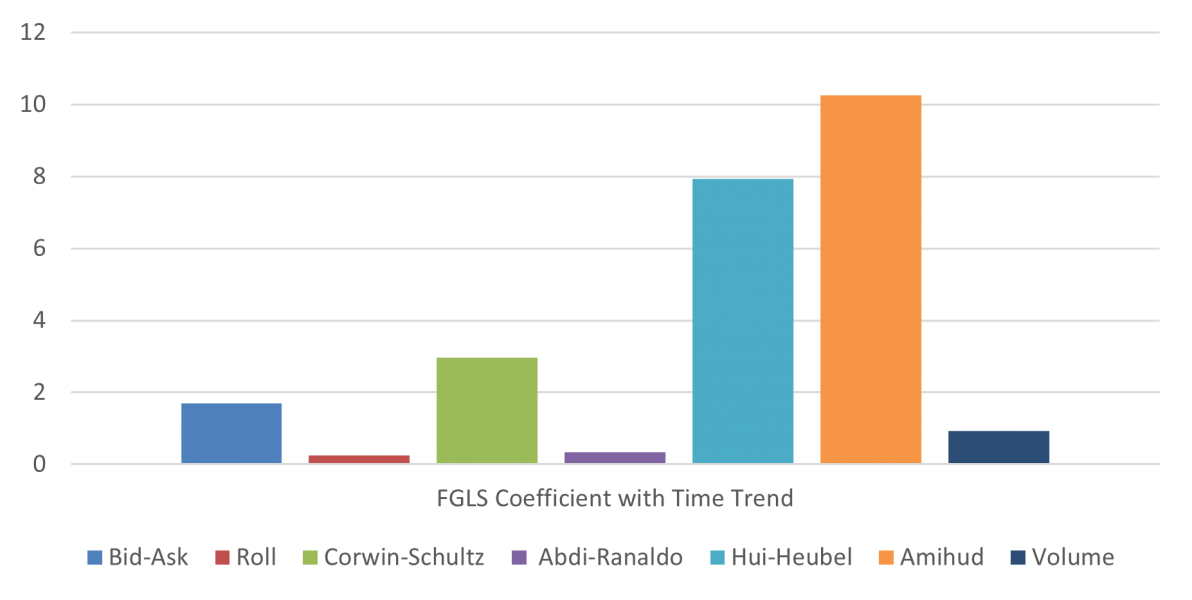
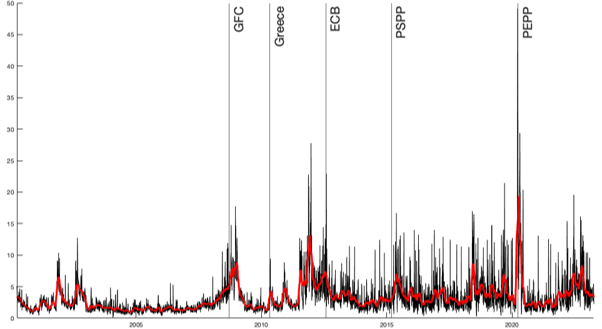
References
Abdi F. and Ranaldo A. (2017). A simple estimation of bid-ask spreads from daily close, high, and low prices. The Review of Financial Studies, 30, 4437-4480.
Altavilla C., Brugnolini L., Gürkaynak R. S., Motto R. and Ragusa G. (2019). Measuring euro area monetary policy. Journal of Monetary Economics, 108, 162–179.
Amihud Y. (2002). Illiquidity and stock returns: Cross-section and time-series effects. Journal of Financial Markets, 5, 31-56.
Corwin S. A., and Schultz P. (2012). A simple way to estimate bid-ask spreads from daily high and low prices. The Journal of Finance, 67, 719-760.
Engle R. F. and Lange, J. (2001). Predicting VNET: A model of the dynamics of market depth. Journal of financial markets, 4, 113-142.
Ferdinandusse M., Freier M. and Ristiniemi A. (2020). Quantitative easing and the price-liquidity trade-off. ECB Working Paper Series No. 2399.
Foucault T., Pagano M., and Röell A. (2013). Market liquidity: theory, evidence, and policy. Oxford University Press.
Goldreich D., Hanke B. and Nath P. (2005). The Price of Future Liquidity: Time- Varying Liquidity in the U.S. Treasury Market. Review of Finance, European Finance Association, vol. 9(1), pages 1-32.
Hui B. and Heubel B. (1984). Comparative liquidity and advantages among major US stock markets. Data Resources Inc. Financial Information Group Study Series, 84081.
Kyle A. S. (1985). Continuous auctions and insider trading. Econometrica, 53, 1315-1335.
Roll R. (1984). A Simple Implicit Measure of the Bid-ask spread In an Efficient Market. Journal of Finance, 39, 1127-1139.