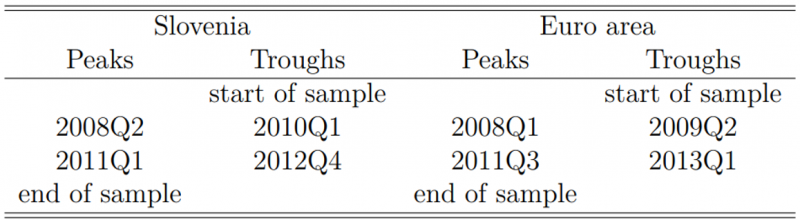
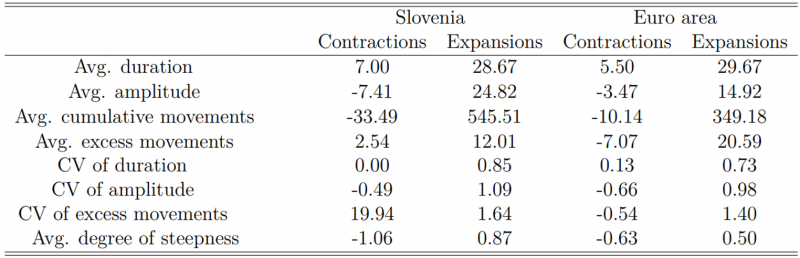
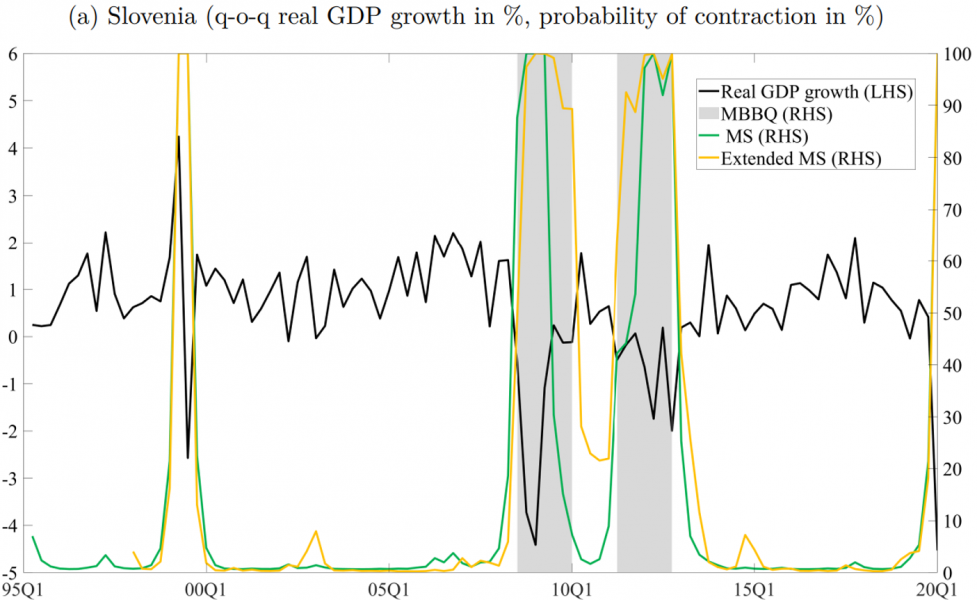
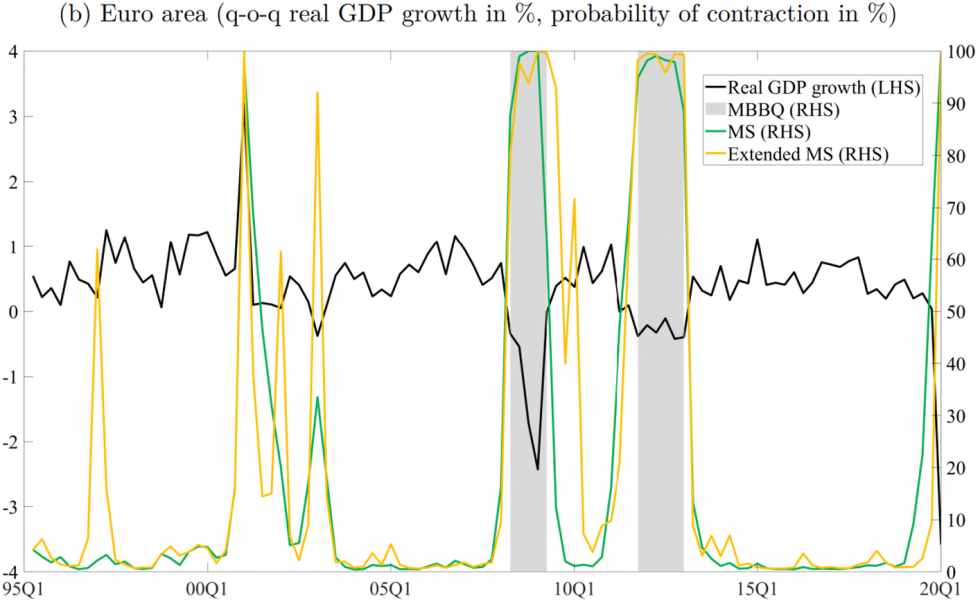
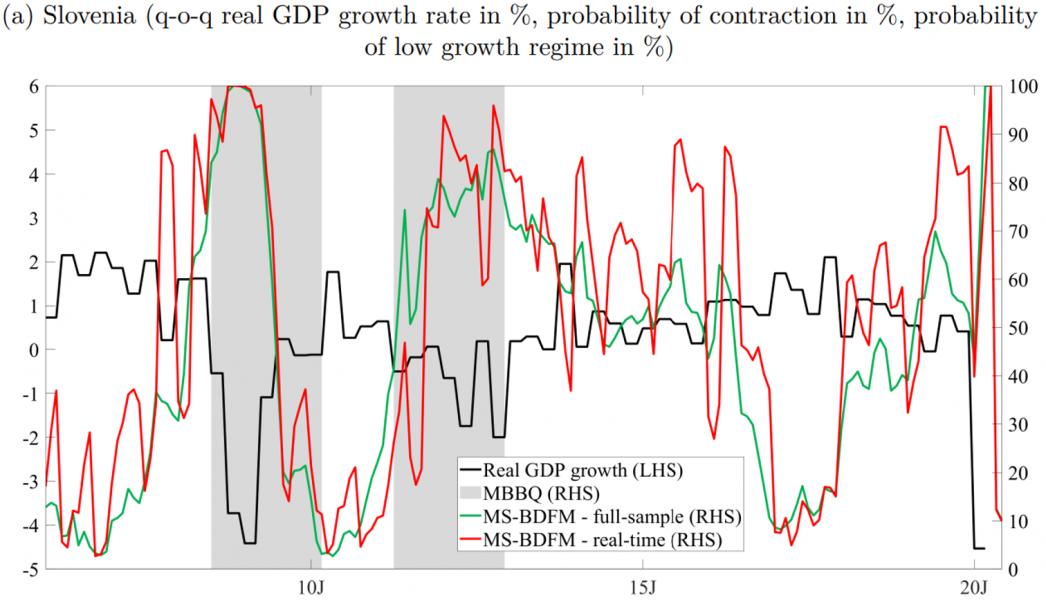
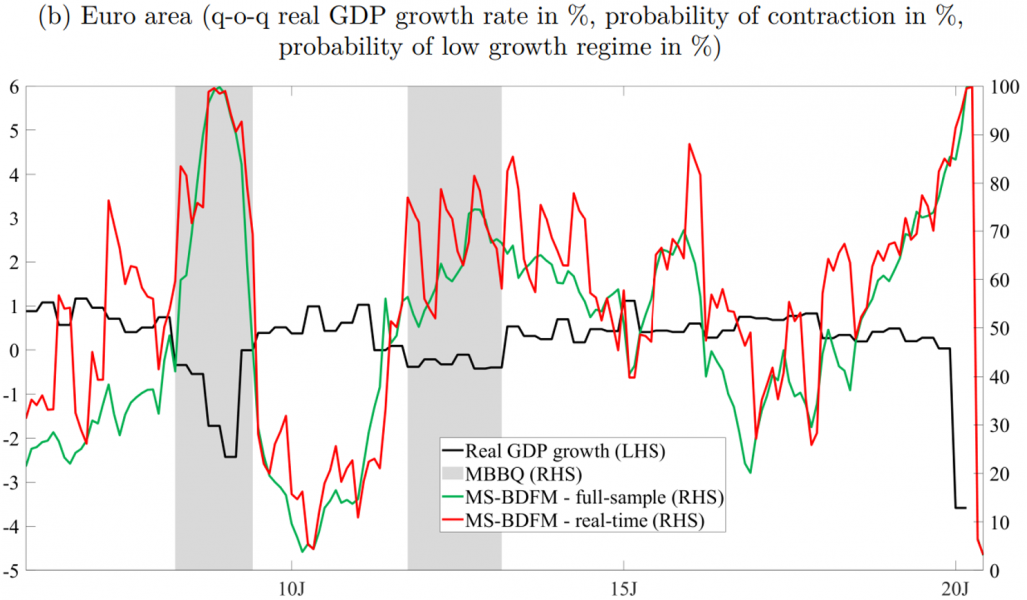
References
Artis, M. J., Marcellino, M., & Proietti, T. (2005). Dating the Euro Area Business Cycle. In L. Reichlin (ed.), Euro Area Business Cycle: Stylized Facts and Measurement Issues (p. 83-93). CEPR.
Bańbura, M., & Modugno, M. (2014). Maximum Likelihood Estimation of Large Factor Model on Datasets with Arbitrary Pattern of Missing Data. Journal of Applied Econometrics, 29(1), p. 133-160.
Bry, G., & Boschan, C. (1971). Cyclical Analysis of Time Series: Selected Procedures and Computer Programs. NBER Books.
Burns, A. F., & Mitchell, W. C. (1946). Measuring Business Cycles. NBER Books.
Camacho, M., Perez-Quiros, G., & Poncela, P. (2013). Short-Term Forecasting for Empirical Economists: A Survey of the Recently Proposed Algorithms. Foundations and Trends® in Econometrics, 6(2), p. 101-161.
Camacho, M., Perez-Quiros, G., & Poncela, P. (2018). Markov-Switching Dynamic Factor Models in Real Time. International Journal of Forecasting, 34(4), p. 598-611.
Chauvet, M., & Piger, J. (2008). A Comparison of the Real-Time Performance of Business Cycle Dating Methods. Journal of Business & Economic Statistics, 26(1), p. 42-49.
Claessens, S. Kose, M. A., & Terrones, M. E. (2012). How do Business and Financial Cycles Interact? Journal of International Economics, 87(1), p. 178-190.
Corsetti, G., Kuester, K., & Müller, G. J. (2016). The Case for Flexible Exchange Rates in a Great Recession. Cambridge Working Papers in Economics 1644.
Diebold, F. X., & Rudebusch, G. D. (1990). A Nonparametric Investigation of Duration Dependence in the American Business Cycle. Journal of Political Economy, 98(3), p. 596-616.
Diebold, F. X., & Rudebusch, G. D. (1991). Turning Point Prediction with the Composite Leading Index: An Ex Ante Analysis. In K. Lahiri & G. H. Moore (eds.), Leading Economic Indicators: New Approaches and Forecasting Records (p. 231-256). Cambridge: Cambridge University Press.
Doz, C., Ferrara, L., & Pionnier, P.-A. (2020). Business Cycle Dynamics After the Great Recession: An Extended Markov-Switching Dynamic Factor Model. OECD Statistics Working Papers 2020/01.
Dupraz, S., Nakamura, E., & Steinsson, J. (2019). A Plucking Model of Business Cycles. NBER Working Papers 26351.
Estrella, A., & Mishkin, F. S. (1998). Predicting U.S. Recessions: Financial Variables as Leading Indicators. The Review of Economics and Statistics, 80(1), p. 45-61.
European Commission (2001). European Economy. Directorate – General for Economic and Financial Affairs, 73.
European Commission (2003). European Economy. Directorate – General for Economic and Financial Affairs, 6.
Giannone, D., Reichlin. L., & Small. D. (2008). Nowcasting: The Real-Time Informational Content of Macroeconomic Data. Journal of Monetary Economics, 55(4), p. 665-676.
Hamilton, J. D. (1989). A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica, 57(2), p. 357-384.
Harding, D. E., & Pagan. A. R. (2002). Dissecting the Cycle: A Methodological Investigation. Journal of Monetary Economics, 49(2), p.365-381.
Harding, D. E., & Pagan. A. R. (2003). A Comparison of Two Business Cycle Dating Methods. Journal of Economics Dynamics and Control, 27(9), p. 1681-1690.
Kim, C.-J., & Nelson, C. R. (1998). Business Cycle Turning Points, a New Coincident Index, and Tests of Duration Dependence Based on a Dynamic Factor Model with Regime Switching. The Review of Economics and Statistics, 80(2), p. 188-201.
Leiva-León, D., Perez-Quiors, G., & Rots, E. (2020). Real-Time Weakness of the Global Economy: A First Assessment of the Coronavirus Crisis. ECB Working Paper Series 2381.
López, M. (2015). Asset Price Bubbles and Monetary Policy in a Small Open Economy. Ensayos Sobre Política Ecónomica, 33, p. 93-102.
Mudambi, R., & Taylor. L. W. (1991). A Nonparametric Investigation of Duration Dependence in the American Business Cycle: A Note. Journal of Political Economy, 99(3), p. 654-656.
Mudambi, R., & Taylor. L. W. (1995). Some Non-Parametric Tests for Duration Dependence: An Application to UK Business Cycle Data. Journal of Applied Statistics, 22(1), p. 163-177.
Ohn, J., Pagan, A. R., & Taylor, L. W. (2004). Testing for Duration Dependence in Economic Cycles. The Econometrics Journal, 7(2), p. 28-549.
Pagan, A. R. (1998). Bulls and Bears: A Tale of Two States. Walras-Bowley Lecture. Montreal: Econometric Society.
Poncela, P., Ruiz, E., & Miranda, K. (2021). Factor Extraction Using Kalman Filter and Smoothing: This is Not Just Another Survey. International Journal of Forecasting, 37(4), p. 1399-1425.
Radovan, J. (2023). An Analysis of Business Cycle Fluctuations in Slovenia and the Euro Area. Banka Slovenije Working Papers 03/2023.
Sila, U., Jemec, N., & Morgavi, H. (2015). Raising Competitiveness and Long-Term Growth of the Slovenian Economy. OECD Economics Department Working Papers 1241.
Stock, J. H., & Watson, M. W. (1989). New Indexes of Coincident and Leading Economic Indicators. In O. Blanchard & S. Fischer (eds.), NBER Macroeconomics Annual 1989, 4 (p. 351-409). Cambridge (Massachusetts): MIT Press.
Stock, J. H., & Watson, M. W. (1991). A Probability Model of the Coincident Economic Indicators. In K. Lahiri & G. H. Moore (eds.), Leading Economic Indicators: New Approaches and Forecasting Records (p. 63-89). Cambridge: Cambridge University Press.
Tasci, M., & Zevanove, N. (2019). Do Longer Expansions Lead to More Severe Recessions? Federal Reserve Bank of Cleveland Economic Commentary 2019-02.