The 2007-2008 financial crisis forced governments to choose between the unattractive alternatives of either bailing out a systemically important bank (SIB) or allowing it to fail disruptively. Bail-in has been put forward as an alternative that potentially addresses the too-big-to-fail and contagion risk problems simultaneously. Though its efficacy has been demonstrated for smaller idiosyncratic SIB failures, its ability to maintain stability in cases of large SIB failures and system-wide crises remains untested. This paper’s contribution is to assess the financial-stability implications of bail-in design, explicitly accounting for the multi-layered networked nature of the financial system. We present a model of the European financial system that captures all five of the prevailing contagion channels. We demonstrate that it is essential to understand the interaction of multiple contagion mechanisms and that financial institutions other than banks play an important role. Our results indicate that stability hinges on the bank-specific and structural bail-in design. On one hand, a well-designed bail-in buttresses financial resilience, but on the other hand, an ill-designed bail-in tends to exacerbate financial distress, especially in system-wide crises and when there are large SIB failures. Our analysis suggests that the current bail-in design may be in the region of instability. While policy makers can fix this, the political economy incentives make this unlikely. In all, our findings indicate that the too-big-to-fail problem remains unresolved today.
Whereas the resolution of (potentially) ailing banks via the bail-in mechanism has already been used with reasonable success on several occasions in recent years, these were mostly for smaller, non-systemically globally important banks (G-SIB) with somewhat idiosyncratic problems (WBG (2016)). Meanwhile, there remain doubts whether this bail-in mechanism would be practical and effective during a systemic crisis (see e.g. Avgouleas and Goodhart (2015), Bernanke (2017)), in which there were general strains on many banks at the same time. This latter question depends in some large part on the various parameters of the bail-in mechanism. When this bail-in process was adopted, in the Bank Recovery and Resolution Directive (BRRD) directive in Europe, and in the Orderly Liquidation provision of the Dodd Frank Act in the United States, quite a lot of leeway was left to the relevant regulators to choose and vary these parameters.
In our accompanying, and much longer, paper, with the main text available in CEPR DP 16509,2 and the associated technical appendices available in SSRN,3 we have tried to investigate the systemic implications of the bail-in design, explicitly taking into account the financial system as a whole. For this, we use as a case study the European financial system in which the BRRD applies. Since the key design parameters for European bail-ins are typically also key parameters in bail-in designs in other jurisdictions, such as the United States, we expect our results to be relevant across jurisdictions even though details of the bail-in process might differ per jurisdiction.
To evaluate the systemic implications of the applicable bail-in design, we build on a multi-layered network model of the European financial system developed by Farmer et al. (2020). In addition, we calibrate this model using S&P Global Market Intelligence data and the 2018 European Banking Authority (EBA) disclosures of the stress test results. The calibrated systemwide stress testing model captures the prevailing contagion mechanisms that could endogenously amplify shocks emanating from bail-ins, i.e. exposure loss contagion, overlapping portfolio contagion, funding contagion, bail-in debt revaluations, and bail-in debt runs originating from concerns over expected losses, uncertainty, or similarity to a recently failed bank, importantly including their interactions.
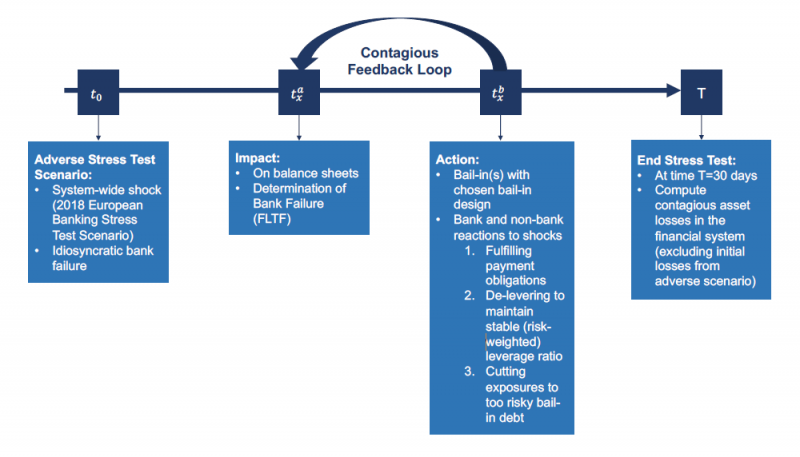
These interactions can be seen diagrammatically in Figure 1, and the timeline of our exercise to model the process, following either a systemwide shock or an idiosyncratic bank failure is shown in Figure 2.
Figure 1: Interaction among Contagion Mechanisms. A bail-in (shown with a lightning bolt) may precipitate interactions between the five contagion mechanisms: exposure losses, revaluations of bail-in debt, halts to roll-overs of bail-in debt, funding contagion and fire sale contagion. These forms of contagion in turn could cause further insolvency-induced or liquidity-induced bail-ins. An exogenous stress scenario may fuel such interactions among contagion mechanisms directly, rather than via the bail-in mechanism, resulting in bail-ins indirectly.
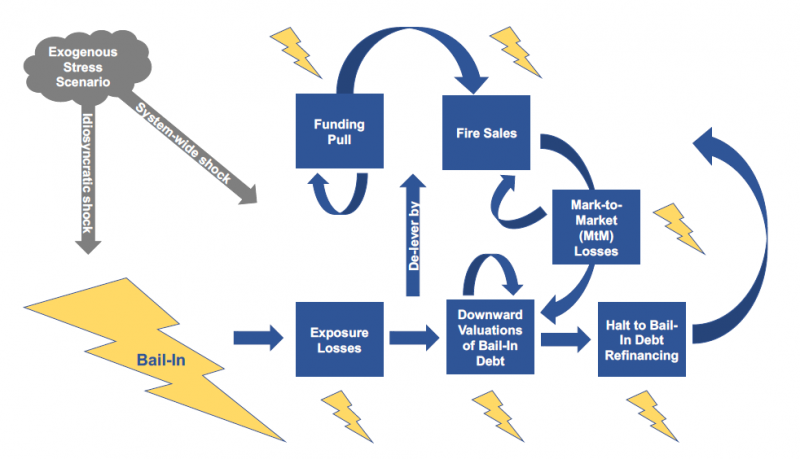
Figure 2: Timeline of the system-wide stress test with bank bail-ins. The stress test starts at time t0 with an exogenous crisis scenario and ends 30 days later at time T = 30. At the time steps tx in between contagion may take place, for x = 1, … , 29. At any sub time step 
the impact of shocks is felt and at step 
action is taken in response to shocks.
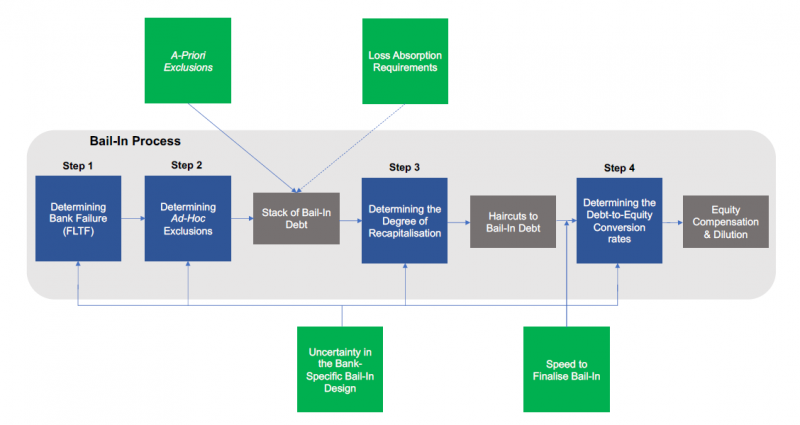
The bail-in design consists of two parts, the bank-specific and structural bail-in design. The bank-specific bail-in design consists of the parameters that the resolution authorities must set for each separate bank bail-in (blue boxes) (see Figure 3). The bank-specific design consists of the failing-likely-to-fail (FLTF) threshold, the ad-hoc debt exclusions, the recapitalisation target, and debt-to-equity conversion rates. Once these four parameters have been specified, the resolution authority knows how to carry out the bail-in of a failing bank. The structural bail-in design consists of the parameters that tend to apply structurally through time and across a set of banks (green boxes) (see Figure 3). The regulator must determine these in advance of any bail-in taking place. The bank-structural design consists of a-priori debt exclusions, loss absorption requirements, uncertainty in the bank-specific bail-in design and the speed to complete a bail-in.
Figure 3: Schematic overview of the bail-in mechanism. The blue blocks denote the parameters of the bank-specific bail-in design and the green blocks the parameters of the structural bail-in design.
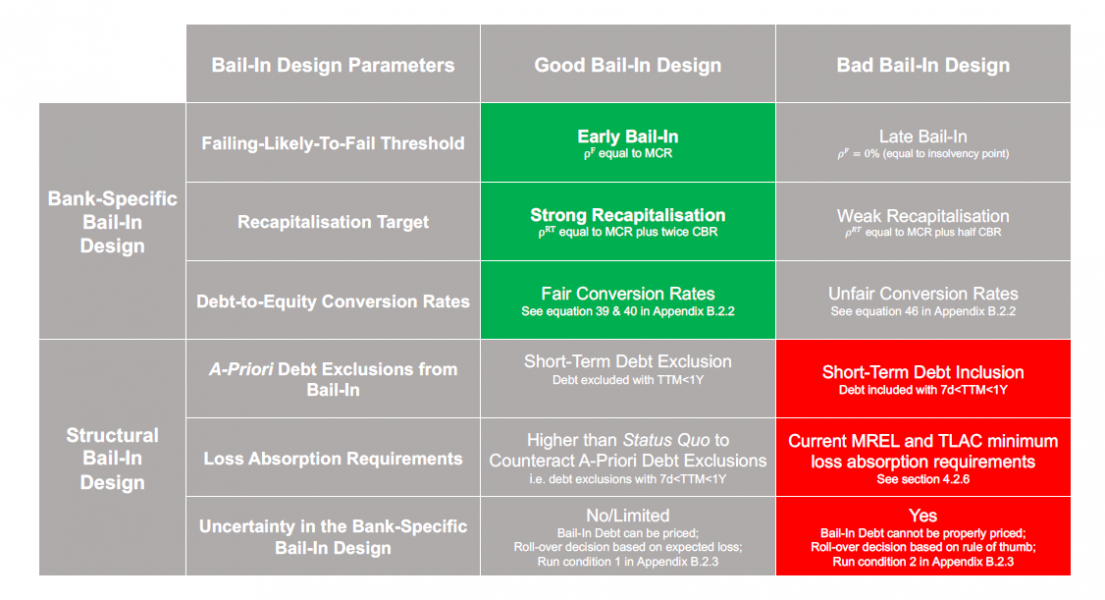
We study different bail-in designs by varying parameters and observing how they affect the response of the financial system to the shocks. The parameter space is too large to investigate exhaustively. We simplify the analysis by identifying two extreme values for each parameter, one corresponding to a “good” bail-in design, and the other corresponding to a “poor” bail-in design. These are roughly bounded by the parameter values that the resolution authority indicates they could plausibly pick, as set out in Section 3 of the main paper. Figure 4 shows the baseline values for the good and poor bail-in design. The key parameters for the bail-in design are given in Figure 4. All results shown are averages over 50 different realizations, corresponding to variations in the randomly reconstructed interbank and common asset holdings networks based on calibrated balance sheets.
Figure 4: The “good” and “poor” baseline configurations of the bail-in design. By default, we show results for the good bank-specific design (highlighted in green) and the poor structural design (highlighted in red). MCR stands for minimum capital requirements 
, CBR stands for combined capital buffer 
and TTM refers to the time to maturity.
What we then did was to study the effects for setting the parameters of bail-in for both extrema, ‘good’ and ‘poor’, on contagious asset losses for the European system, separately for the banks specific parameters and then for the structural parameters as a group. Then within each group we looked at the individual effects of each constituent parameter on such contagious losses.
This has involved a large number in numerical exercises, and there is only space in this note to go through the three that we consider most salient. These are the effects of the choice of the set of good or poor bank-specific design parameters and then the choice within that first set of the failure threshold and then, second, of the recapitalisation threshold.
Let us start with the set of specific design parameters shown in Figure 5.
Figure 5: The stability implications of the bank-specific bail-in design. Shows the systemic response for idiosyncratic shocks and for the EBA shock. The blue line uses good and the orange line uses the poor bank-specific parameters. Both lines use the poor structural parameters.
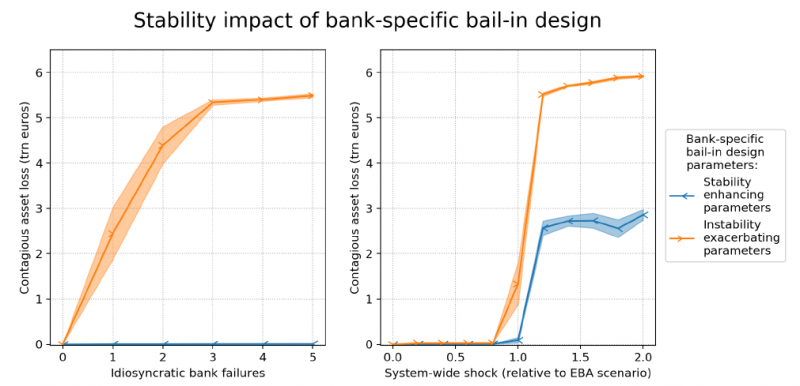
Figure 5 shows how the financial system responds to shocks differently for a bank-specific bail-in design with the good and poor bank-specific parameters, keeping the structural parameters equal to their default (poor) setting. The left panel shows the systemic response to idiosyncratic shocks and the right panel shows the systemic response to the 2018 EBA stress test. The magnitude of the systemic loss to the banking system is measured in trillions of euros. The asset loss shown is only the contagious loss, i.e. we do not include the exogenously imposed shocks in either case. We observe that when both the poor bank-specific and poor structural parameters are applied the system’s loss can reach up to 6 trillion euros, whereas when the bank-specific parameters are turned to their good values system losses stay below 3 trillion dollars in extreme system-wide crisis and stay close to zero when multiple banks idiosyncratically fail. To put these results in perspective, the size of European banking system that we model is 22 trillion euro, so 6 trillion euros represents 27.3% of the system value. By comparison, the asset losses emanating directly from the endogenously imposed EBA shock are only about 0.3 trillion euro.
Figure 5 reveals how the choice of the bank-specific design parameters greatly alters systemic risk by a, perhaps surprisingly, large magnitude of multiple trillions of euros (compare orange and blue lines). On the one hand, we observe that “good” bank-specific parameters consisting of an early bail-in, strong recapitalization, and fair conversation rates almost eliminate contagion in the case of idiosyncratic failures of large SIBs (blue line, left plot). Yet, the good parameters curb but do not crush contagion in the case of increasingly severe system-wide distress (blue line, right plot). On the other hand, we observe that “poor” bank-specific parameters consisting of a late bail-in, weak recapitalization and unfair conversion rates precipitate contagion in the case where large SIBs idiosyncratically fail (orange line, left plot) and exacerbate financial turmoil in case of a systemic crisis (orange line, right plot). In contrast, the bank-specific bail-in design is inconsequential if smaller SIBs idiosyncratically fail (as shown in Figure 19 of the Online Appendix).
Figure 6: The stability implications of the choice of failure threshold. Shows the systemic response varying the failure threshold. All other bank-specific parameters are set to their good values. As before, structural parameters are set to poor values.
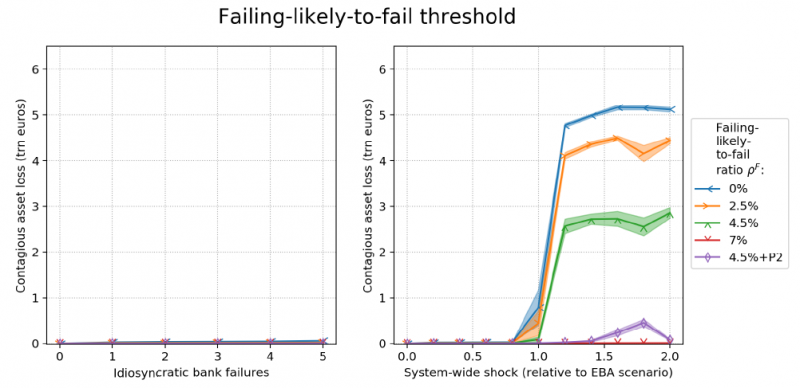
Figure 6 studies the stability impact of the failing-likely-to-fail threshold, other parameters being held constant. Contagion is higher if the bank is bailed-in only once it has become insolvent (blue line) than when it is bailed-in earlier, for instance at its Pillar I minimum capital requirements of 4.5% of CET1 equity relative to RWAs (green line). Contagion is even lower if that bank is bailed-in even earlier, for example at its Pillar I and II minimum capital requirements (purple line). Contagion kicks in non-linearly in the right plot only once the system-wide shock becomes sufficiently severe. Before that severity our analysis shows that the shock is not large enough to trigger bail-ins, precautionary de-levering or exposure reductions to bail-in debt (plots not shown). Contagious losses can increase non-linearly as a function of the adverse shock because of shock amplifications in the financial system (see e.g. Cont and Schaanning (2017), Aymanns et al. (2018)).
Contagion remains small, in the order of multiple millions, in the case of idiosyncratic failures (left plot) irrespective of the level of the FLTF threshold. The reason is that as long as the other bank-specific parameters are well-designed and all surviving banks are well capitalized, the exposure losses resulting from a bail-in of an idiosyncratically failing SIB do not trigger further bail-ins or precautionary action (analysis plots not shown). Contagion in this case does not extend beyond exposure losses resulting from the idiosyncratic bail-ins. In the case that the other bank-specific bail-in parameters are ill-designed – i.e. weak recapitalisation and unfair conversion rates – then the level of FLTF threshold starts to also matter greatly in the case of idiosyncratic bank failure.
These observations point to our finding that the later a bank is bailed-in (i.e. the lower the FLTF threshold is set), the higher the system’s contagious losses are. The reasons why an earlier bail-in promotes stability are twofold. The less important but obvious reason is that a bank that is bailed-in earlier requires fewer haircuts to be recapitalised to a given recapitalisation target, thereby limiting the potential scope of exposure losses to the bank’s creditors which could spur further contagion. The more important but non-obvious reason is that banks that are bailed-in early enough such that they remain solvent at the onset of bail-in can have their creditors compensated with an equal amount of equity (in book value terms) per incurred haircut without breaching the “No-Creditor-Worse-Off” (NCWO) principle, thereby avoiding net exposure losses altogether at the point of conversion. Hence, an early bail-in can limit contagion. The NCWO principle states that resolution authorities should seek to ensure that no creditor or shareholder is expected to incur greater net losses than it would have incurred in winding up the bank under normal insolvency proceedings.4
Figure 7 studies the stability impact of the recapitalisation target, again with other parameters held constant and equal to their baseline value. Contagion remains more limited if the bank is recapitalised strongly, for instance to its minimum capital ratio plus twice its combined capital buffers (brown line), than if it is recapitalised weakly, for example to its minimum capital ratio (blue line). Note that we included the blue line, which is worse than the orange line corresponding to the poor bank-specific baseline, since regulators could plausibly recapitalise a bank to just its minimum capital requirement. Unlike in the previous plot, contagion now also amplifies non-linearly in the case of idiosyncratic bank failures with a poor recapitalisation target choice (orange and blue line). The reason is that a weakly recapitalised bank will be prone to de-lever and repeated failure in our model, thereby imposing losses on others who are then be dragged into preventative action or a bail-in, resulting in further contagion.
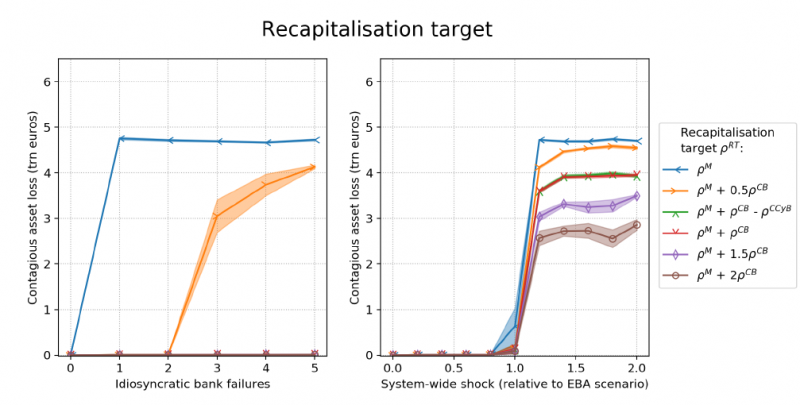
Contagion remains more limited, if bailed-in banks are more strongly recapitalised. Superficially, one might have guessed that a stronger recapitalisation undermines stability, since a higher recapitalisation results in more haircuts increasing the scope for exposure losses that could ignite further contagion. So why does a stronger recapitalisation reduce systemic risk? Part of the answer is that a stronger recapitalisation means that a bank finds it easier to retain access to funding in our model and keep its funding cost low (latter not modelled). This part is well-understood in the literature (see e.g. Burrows et al. (2012)). In our model bail-in debt is priced (using a novel method) and creditors stop rolling over maturing funding to bail-in debt that is expected to suffer great losses. The other part of the answer is that a stronger recapitalisation means that a bank in our model has less incentives to de-lever to attain a more resilient capital ratio, one that is further removed from its minimum capital ratio where failure is likely.
A point that is insufficiently appreciated so far by resolution authorities, however, is that recapitalising a bank quite strongly such that it meets both its minimum capital requirements plus its combined capital buffers might still compromise stability on the order of trillions of dollars (compare red line with purple or brown line). The reason is that a bank may not be willing to use its regulatory capital buffers (Goodhart et al. (2008), Goodhart (2013), Farmer et al. (2020), FED (2020), Kleinnijenhuis et al. (2020)), because buffer use comes with penalties in its ability to make discretionary payments such as dividends and bonuses. A bank that is thus recapitalised to the edge of its buffer zone will, with any further exogenous or contagious asset loss, be inclined to de-lever to get out of the penalty zone. Especially in a crisis, it is highly likely that a bank will suffer further losses triggering it to de-lever. In our model, a bank starts de-levering once it has used 50% of its regulatory buffers. Though de-levering might be individually rational, it tends to be destabilising for the system as a whole. In sum, the novel point is that banks should be recapitalised sufficiently in excess of their minimum capital requirements and regulatory buffers (see e.g. purple and brown line) so that they are unlikely to de-lever or suffer funding outflows following the bail-in.
A second point that is not sufficiently appreciated is that a greater amount of haircuts to meet a higher target does not necessarily imply greater net losses for creditors. With “fair” conversation rates, creditors in the recapitalisation phase of the bail-in can be compensated fully, resulting in net losses zero at the point of conversion.5 Therefore, a higher recapitalisation target will not exert a strong destabilising pressure via the exposure loss channel if conversion rates are fair and bail-in happens early.
We have shown that an early bail-in promotes stability. Many other economists, who have studied financial regulation, such as in Evanoff and Kaufman (2005), Claessens, et al., (2010), and Benston, et al., (1986), have also argued strongly for structured early intervention. Yet EU and US regulators are prone to bail-in a bank late. US regulators explicitly plan to bail-in a bank late, only when it is or nearly is insolvent (McAndrews et al. (2014)). EU regulators, though legally required to bail-in a bank early when it breaches its minimum capital requirements, may, in practice, bail-in a bank so late that it is close to insolvency. As noted, one reason is that suffered losses are often recognised belatedly. Another is that a bank’s asset value may fall sharply due to a sudden asset loss in a crisis. This suggests setting the FLTF threshold sufficiently high such that, even if unrecognised losses are discovered and asset value uncertainty prevails, a bank will typically be found to be solvent at the onset of bail-in. A final important reason for tending to bail-in a bank late is that it is in the short-term interest of bank’s stakeholders (Avgouleas and Goodhart (2015)). The basic problem is that the incentive structure for almost all those closely involved leads them in the opposite direction from bailing-in early. Complementing the regulatory failure trigger with a market-based one may combat the tendency to bail-in too late. An alternative is a metric based on multiple requirements, see Buckmann et al. (2021).
There is no such thing as a fool proof, or perfectly accurate, valuation of a bank, or any other holders’, assets. The current value of an asset depends on the future returns that it will bring, discounted back to the present, but the future path of such returns, (and of future interest rates), is unknown, and unknowable, though it is perfectly possible to estimate probabilities, at least up to a point. Indeed, the market value of assets, interacting with their volatility, can be used to make estimates of the distance to, or probability of, default; and, indeed, of the likelihood of any such default having a contagious effect on other similar institutions (Segoviano and Goodhart (2009)). Indeed, such estimates of DD, or PD, have, in the past at least, been a considerably more accurate predictor of actual defaults than accounting valuations.
Nevertheless, they are not, and cannot, be entirely accurate, and, if they were used as policy triggers, they would surely be subject to even greater manipulation than at present (Goodhart’s Law, Goodhart (1975)). So, if a regulator was to trigger a failure threshold based on a somewhat mechanical algorithm based on market valuations, and volatilities, it would almost certainly be subject to lawsuit, claiming that the algorithms and valuations were either inherently faulty or inappropriate. The last thing that regulators want is to have each failure leading to a long-drawn-out legal battle. And if they were to lose such a battle, as might occur, their credibility would be shot, whereas the failing bank has no such constraint.
Indeed, for such reasons, the failure of a bank is hardly ever triggered early by an assessment of its solvency, whether based on market or accounting values. Instead, what normally happens is that various signals, including market valuations, lead informed investors to believe that a bank may be subject to possible failure; so, to avoid loss and having their claim frozen, they withdraw funding. The normal sequence of failure is that a bank thus becomes illiquid, and appeals to the central bank for liquidity support, almost always claiming that it is fully solvent. The scale of support needed in the context then causes the regulatory authorities to send in an independent valuer, (“valuation one” in the process), who must be independent from any public authority, to inform the FLTF criteria. And it is this valuation that typically leads the regulatory authority to claim, at a late stage, that the failure threshold is triggered.
Another concern about triggering a failure threshold early is that this could well lead the market in turn to reduce the exposure to whichever bank is the next weakest “antelope in the herd” (Blinder (2013)), especially if there is pronounced uncertainty over the losses creditors could suffer in a prospective bail-in. So, after Bear Stearns, the market focused on Lehman Brothers; after Lehman Brothers, Merrill Lynch; and after Merrill Lynch, everyone else; with a similar story occurring after Northern Rock in the UK. With regulators, like bank managers, having relatively short periods in office, there is a natural inclination to defer taking a step which could have serious and widespread consequences, in the hopes that (market) conditions might improve, and the need for resolution may go away; or, at least, be deferred until someone else takes up position.
We also demonstrated that a strong recapitalisation fortifies resilience. Yet none of the three recapitalisation options advanced by the BRRD recapitalises a bank sufficiently; these being recapitalisation to make a bank meet its minimum capital requirements; recapitalisation to bring the bank’s capital ratio into line with its peers; and recapitalisation to ensure a bank also meets its regulatory buffers. All three are too weak. And so is the recapitalisation target proposed under BRRD II, which is equalled to a bank’s minimum capital requirement plus its combined regulatory buffer minus its applicable countercyclical capital buffer. Instead, a bank should be recapitalised more than both its minimum capital requirements and its regulatory buffers. This permits the bank to suffer inevitable further losses in a systemic crisis without being pushed into the regulatory buffer zone, where it will be inclined to act in destabilising ways to de-lever in order to avoid restrictions on discretionary payments and stay away from default, as shown in the results. This also reduces the risk of continued funding outflows following the bail-in. Recapitalisation to a level where a bank’s capital ratio outstrips comfortably both its minimum requirements and regulatory buffer standards is shown to be a good design choice boosting stability. But this is unlikely to happen. The recapitalisation target requires that it complies with the conditions for continued authorization and sustains or regains market confidence. This, obviously, is a somewhat subjective matter, and leaves a lot of leeway for the concerns and incentives of those involved.
The higher the recapitalisation target ratio is, the more the equity shareholders will be diluted, and the less their expected returns. Similarly, the other bail-in creditors will suffer greater haircuts if a high target is imposed. This will generate a net loss if their haircut is not compensated fully with a debt-to-equity swap. Even if creditors do not encounter net losses because of the swap, the swap exposes the new equity holders to any future losses by being thrust to the bottom of the claim hierarchy. Some creditors for this reason will not like holding equity. Others may not be allowed institutionally to hold equity. So, for all these reasons, those involved in the commercial banking sector will pressurise the regulators, and the politicians, to impose as low a recapitalisation target as seems consistent with a reasonable chance of successful recovery.
Our study had the following main results.
In all, our findings indicate that the too-big-to-fail problem remains unresolved today.
Avgouleas, Emilios, and Charles Goodhart. “Critical reflections on bank bail-ins.” Journal of Financial Regulation 1, no. 1 (2015): 3-29.
Aymanns, Christoph, J. Doyne Farmer, Alissa M. Kleinnijenhuis, and Thom Wetzer. “Models of financial stability and their application in stress tests.” In Handbook of Computational Economics, vol. 4, pp. 329-391. Elsevier (2018).
Benston, George J., Robert A. Eisenbeis, Paul Horvitz, Edward J. Kane, and George Kaufman. “Perspectives on safe and sound banking: Past, Present and Future.” MIT Press (1986).
Bernanke, Ben. “Why Dodd-Frank’s orderly liquidation authority should be preserved.” Brookings Institute. February 28 (2017).
Blinder, Alan S. After the music stopped: The financial crisis, the response, and the work ahead. No. 79. Penguin Group USA, 2013.
Buckmann, Marcus, Paula Gallego Marquez, Mariana Gimpelewicz, Sujit Kapadia, and Katie Rismanchi. “The more the merrier? Evidence from the global financial crisis on the value of multiple requirements in bank regulation.” (2021).
Burrows, Oliver, David Learmonth, Jack McKeown, and Richard Williams. “RAMSI: a top-down stress-testing model developed at the Bank of England.” Bank of England Quarterly Bulletin (2012): Q3.
Claessens, Stijn, Richard Herring, Dirk Schoenmaker, and Kimberly A. Summe. “A safer world financial system: Improving the resolution of systemic institutions”. Geneva: International Center for Monetary and Banking Studies (2010).
Cont, Rama, and Eric Schaanning. “Fire sales, indirect contagion and systemic stress testing.” Indirect Contagion and Systemic Stress Testing (June 13, 2017) (2017).
Evanoff, Douglas Darrell, and George G. Kaufman, eds. “Systemic financial crises: resolving large bank insolvencies”. World Scientific (2005).
Farmer, J. Doyne, Alissa M. Kleinnijenhuis, Paul Nahai-Williamson, and Thom Wetzer. “Foundations of system-wide financial stress testing with heterogeneous institutions.” Bank of England Working Paper (2020).
FED (2020), “SR 20-5: Questions and answers (Q&A) on statement regarding the use of capital and liquidity buffers”, Federal Reserve Board https://www.federalreserve.gov/supervisionreg/srletters/sr2005.htm
Goodhart, Charles AE. “Problems of monetary management: the UK experience.” In Monetary theory and practice, pp. 91-121. Palgrave, London (1984).
Goodhart, Charles. “Liquidity risk management.” Banque de France Financial Stability Review 11 (2008): 39-44.
Goodhart, Charles. “Ratio controls need reconsideration.” Journal of Financial Stability 9, no. 3 (2013): 445-450.
Kleinnijenhuis, Alissa, Laura Kodres, and Thom Wetzer. “Usable bank capital.” VoxEU. org. URL https://voxeu.org/article/usable-bank-capital (accessed 10.26. 20) (2020).
McAndrews, James, Donald P. Morgan, João AC Santos, and Tanju Yorulmazer. “What Makes Large Bank Failures So Messy and What to Do about It?.” Economic Policy Review, Forthcoming (2014).
Segoviano Basurto, Miguel, and Charles Goodhart. “Banking stability measures.” (2009).
World Bank Group. Understanding Bank Recovery and Resolution in the EU: A Guidebook to the BRRD. World Bank, 2016.
J. Doyne Farmer, University of Oxford, Institute for New Economic Thinking at the Oxford Martin School, Mathematical Institute, Doyne.Farmer@inet.ox.ac.uk; Charles Goodhart, London School of Economics, Financial Markets Group, caegoodhart@aol.com; Alissa M. Kleinnijenhuis, Stanford University, Stanford Institute for Economic Policy Research, amklein@stanford.edu.
See here: https://cepr.org/active/publications/discussion_papers/dp.php?dpno=16509.
See here: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3913704.
See: Article 74(2) of the BRRD.
Conversion rates are referred to as fair whenever creditors in the loss absorption phase (i.e. the phase to wipe out insolvency) obtain a pure write down of their debt and creditors in the recapitalisation phase (i.e. the phase to recapitalise the bank further to target) of the bail-in obtain an equity share equal in book value terms to their haircut. These conversion rates are referred to as “fair” since they typically distribute bail-in losses most fairly, while still typically complying with the NCWO principle. By contrast, “proportional conversion rates”, where each creditor in the bail-in receives the same conversion rate, often do not satisfy the NCWO principle.
