

See e.g. Holston, Laubach and Williams (2023), Holston, Laubach and Williams (2017) or Brand, Bielecki and Penalver (2018).
E.g. the Federal Reserve released a revised Statement on Longer-Run Goals and Monetary Policy Strategy in 2020. The Eurosystem concluded its strategy review in 2021. The Bank of Canada renewed its flexible inflation-targeting framework in 2021. The Bank of Japan has conducted a smaller policy review in the beginning of 2021.
Other possibilities to mitigate the ELB constraint in the realm of monetary policy include negative interest rates, forward guidance, and asset purchase programmes.
For survey evidence, see e.g. Coibion, Gorodnichenko and Kamdar (2018). For experimental evidence, see e.g. Afrouzi, Kwon, Landier, Ma and Thesmar (2023).
The extended path algorithm is described in Fair and Taylor (1983). We implement the computations with the software package Dynare, see Adjemian, Bastani, Juillard, Karamé, Maih, Mihoubi, Mutschler, Perendia, Pfeifer, Ratto and Villemot (2021).
The arguments in the loss function are the volatility of price inflation, wage inflation, and the output gap.
We consider a demand shock in the form of a discount factor shock and a supply shock in the form of a technology shock.
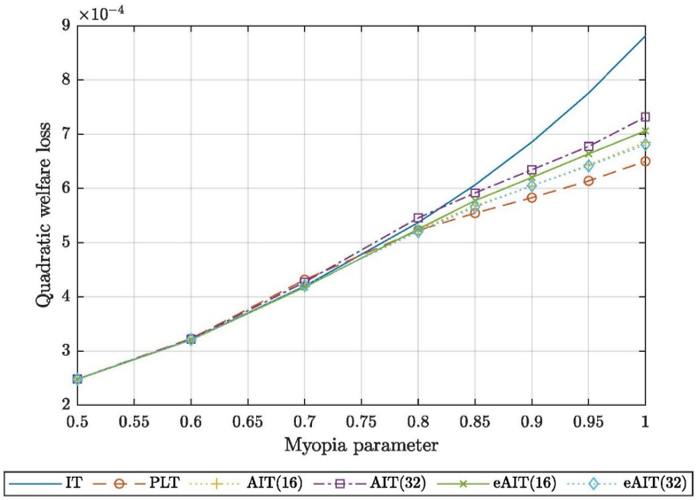
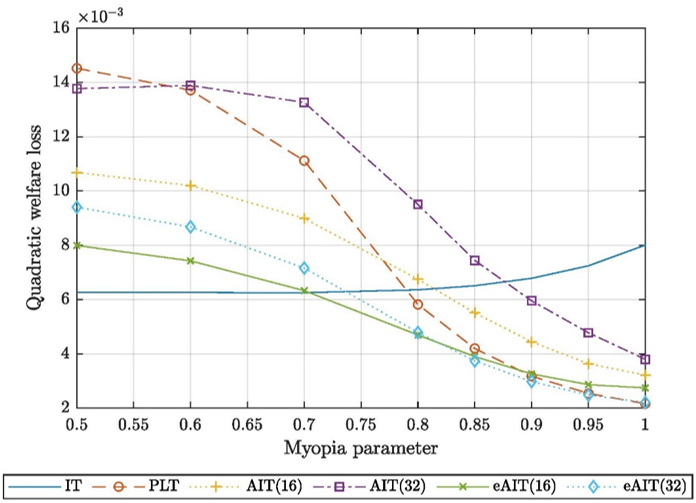
eAIT(32) in the figures represents an eAIT rule with a relatively high exponential smoothing parameter, while eAIT(16) represents an eAIT rule with a lower exponential smoothing parameter. The numbers are, however, not comparable to the averaging windows in the conventional AIT rules.