

Fabo, Jancokova, Kempf and Pastor (2021) use OLS regression to show that central bankers report quantitatively larger effects of QE on output and inflation than academic researchers. We reject the null hypothesis of a Gaussian distribution of the residuals in many of these specifications, except for the language regressions. We then repeat the analysis with regression estimators that are robust to a non-Gaussian residual distribution where this is feasible. We use the median regression and the MS regression estimator. With these robust regression approaches, the null hypothesis that central bank and academic researchers report the same quantitative effect of QE on output and inflation cannot be rejected, with point estimates which are less than half as large. This statistical challenge suggests that more research is required to better understand whether central bank researchers report different QE multipliers or not.
Fabo, Jancokova, Kempf and Pastor (2021) provide the first comparison of the effects of QE reported by central bank1 and academic researchers. They find that central bank researchers report larger inflation and output effects of QE than researchers in academia. Central bank researchers are more likely to report significant results, derive a career benefit from their work and use more positive language to describe their findings. In other words central bankers seem to be parti pris. The underlying tool used by Fabo et al. (2021) is OLS regression and our concern is that this approach may lead to substantial distortions when applied to data sets with substantial outliers. This problem is not avoided by the use of robust standard errors.
We show that the residuals of most of their regressions have values of skewness and kurtosis which are inconsistent with a standard Gaussian distribution. Applying the OLS estimator in these circumstances can lead to biased estimates of statistical significance. We revisit their analysis with regression estimators which are robust to residuals with a non-Gaussian distribution. Once these estimators are adopted, the null hypothesis that central bank and academic researchers report the same inflation and output effects of QE cannot be rejected in most specifications. Their findings on sentiment and career progression are, however, shown to be robust.
Fabo et al. (2021) collect the output and inflation effects of QE from 54 different studies of QE. They also collect information on the authors’ affiliations, their experience and career outcomes. We use the data from appendix A in their paper. We are able to replicate the summary statistics table of their paper. All the statistics match those reported in their paper.2 However, the fourth moment, kurtosis takes some values quite incompatible with the normal distribution. This means that these variables are lepto-kurtic- that is they have much fatter tails, with higher probability of outliers, than would be expected from a normal distribution. Of course, what matters is whether the lepto-kurtic nature of the dependent variables translates into lepto-kurtic (non-Gaussian) residuals. This is what we investigate.
There are three types of outliers which can affect both the estimate and inference in the standard OLS regression framework (see Rousseeuw and Leroy (2003) for more detail). Good leverage points are outliers which are on the regression line, but far away relative to all the other observations. Good leverage points affect only inference and not OLS estimates. On the other hand, observations, which are away from the regression line in y space only, referred to as vertical outliers, affect OLS estimates. Similarly, observations which are outliers in x space, referred to as bad leverage points, affect OLS estimates as well.
The issue is visible in figure 1 where we show the frequency distribution of the impact of QE policies on GDP. The outlying observations, which are all associated with central bank affiliations are clear in the chart. These represent vertical outliers because the policy effect is the dependent variable. Our point is not that these are irrelevant to the estimation of the effect but rather that, unless they are addressed they distort conclusions about the significance of the relationship between central bank affiliation and the effects of QE on the variables in question.
Figure 1: Outliers in regressions of Inflation/GDP effects of QE on central bank affiliation
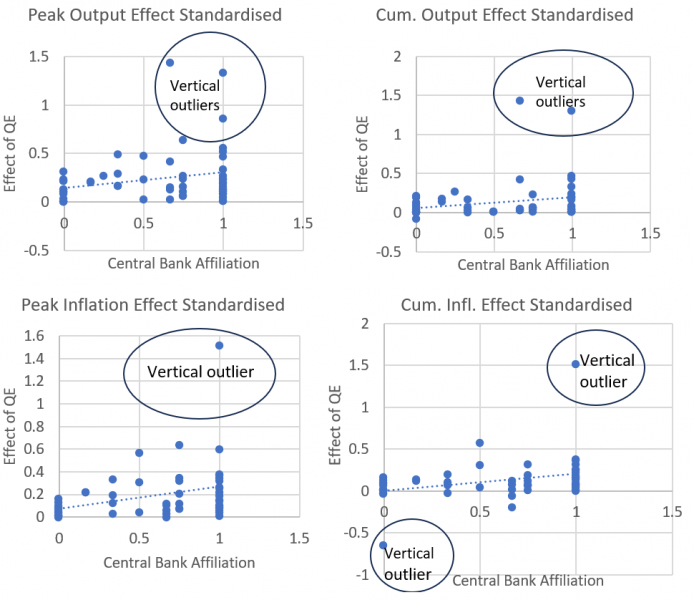
Edgeworth (1887) provided a means of addressing outliers which affect OLS estimates, by introducing the least absolute deviation or median regression estimator. Rather than minimising the sum of squares of the residuals, this estimator minimizes the sum of absolute deviations of the residuals. As the OLS estimator minimises the sum of the squared residuals, any outlying observation will get a large weight, and the greater the outlier, the greater the weight put on this observation. In contrast, the median regression estimator minimises the sum of the absolute errors, putting an equal weight on each observation. However, the caveat of this estimator is that it protects only against vertical outliers, but not against bad leverage points.
An alternative class of robust estimators builds on the idea of using loss functions other than the OLS square and absolute deviation (median regression) estimator. This idea was initially advocated by Huber (1964) who proposed the M estimator. The latest evolution of the approach is the MM estimator proposed by Yohai (1987). The advantage of this estimator is that it has both high efficiency if the underlying distribution is Gaussian and a high breakdown point of 50%, meaning that this estimator resists contamination if outliers comprise up to 50% of observations in the sample. Furthermore, this estimator is robust to all three types of outliers: vertical outliers, good leverage points and bad leverage points. However, when dummy variables are present in the specification, Verardi and Croux (2008) recommend the MS-estimator of Maronna and Yohai (2000). We use the MM-estimator for the specifications without dummy variables and rely on the MS-estimator where dummy variables are present in the regression specification.
The results exploring the statistical significance of a central bank affiliation on the estimate of the output effect of QE show that using OLS regression central bank affiliation generally has a significant effect. The use of OLS, however, invariably leads to a value of the Jarque-Bera statistic which points to a major departure from normality. While this might not matter in a large sample, it raises the risk that the estimated standard errors and thus the p-values of the regression equation are badly distorted.
When we use either median regression or MM/MS regression we do not find statistically significant results. This highlights the risk that the OLS findings may be an artefact of the distribution of the estimates of the different researchers rather than a robust statistical finding. However, more research on this topic is clearly still required to understand whether that is the case or not.
Bertrand, M., E. Duflo, and S. Mullainathan (2004). “How much should we trust differences-in-differences estimates?”. Quarterly Journal of Economics. Vol. 119. Pp 249-275.
Edgeworth, F. (1887). “On observations relating to several quantities”. Hermathena. Vol 6. Pp 279-285.
Fabo, B., M. Jančokova, E. Kempf and L. Pástor (2021) “Fifty shades of QE: comparing findings of central bankers and academics”. Journal of Monetary Economics. Vol. 120. Pp. 1-20. https://doi.org/10.1016/j.jmoneco.2021.04.001.
Huber, P. (1964). “Robust estimation of a location parameter”. Annals of Mathematical Statistics. Vol. 35. Pp. 73-101.
https://www.jstor.org/stable/2238020.
Koenker, R. and G. Bassett. (1978). “Regression quantiles”. Econometrica. Vol 46. Pp. 33-50.
Maronna, R. and V. Yohai. (2000). “Robust regression with both continuous and categorical predictors” Journal of Statistical Planning and Inference. Vol. 89. Pp 197-214.
MacKinnon, J.G. and M.D. Webb (2017). “Pitfalls when estimating treatment effects with clustered data”. The Political Methodologist. Vol. 24. Pages 20-31.
Rousseeuw P and A. Leroy. (2003). Robust regression and outlier detection. Wiley. Hoboken.
Veradi, V. and C. Croux. (2009). “Robust regression in Stata”. Stata Journal. https://doi.org/10.1177/1536867X0900900306.
Weale M. and T. Wieladek. (2016). “What are the macroeconomic effects of asset purchases?”. Journal of Monetary Economics. Vol. 79. Pp. 81-93.
Wu, C. F. J.(1986). “Jackknife, bootstrap and other resampling methods in regression analysis”. Annals of Statistics. Vol. 14. Pp. 1261-1295.
Yohai, V. (1987). “High breakdown-point and high efficiency robust estimates for regression”. Annals of Mathematical Statistics. Vol. 15. Pp 642-656. https://www.jstor.org/stable/2241331.
Our paper (Weale and Wieladek, 2016) was published while we worked at the Bank of England and is included in the study by Fabo et al. (2021). Haldane et al. (2016) and Wieladek et al. (2016) are included papers written by Tomasz Wieladek.
With one very slight difference that we attribute to rounding.