Monetary policy rules: model uncertainty meets design limits

Optimal monetary policy studies typically rely on a single structural model and identification of model-specific rules that minimize the unconditional volatilities of inflation and real activity. In our proposed approach, we take a large set of structural models and look for the model-robust rules that minimize the volatilities at those frequencies that policymakers are most interested in stabilizing. Compared to the status quo approach, our results suggest that policymakers should be more restrained in their inflation responses when their aim is to stabilize inflation and output growth at specific frequencies. Additional caution is called for due to model uncertainty.

Which interest rate rule should a central bank follow? The common way to answer this question is to take a structural macroeconomic model, choose a loss function that approximates the central bank’s preferences (a weighted average of the unconditional variances of inflation and real activity), and find the interest-rate (Taylor) rule coefficients that minimize the loss function. This approach has two drawbacks.

First, according to the standard view, monetary policy through interest-rate setting should not be used as an instrument to fine-tune high-frequency fluctuations of inflation and real activity (Lagarde, 2021 and Powell, 2021) or promote long-term economic growth (Mester, 2023), but rather to smooth cyclical fluctuations. Policymakers should thus aim at stabilizing specific frequencies – not the unconditional volatility – of inflation and real activity. Furthermore, the literature on design limits in macroeconomics has shown that the choice of a policy rule yields a frequency-by-frequency variance trade-off, whereby reducing the variance of targeted variables at certain frequencies may increase the variances at other frequencies (see e.g. Onatski and Williams, 2003, Brock et al., 2007, and Brock et al., 2013). Policymakers have to be aware and informed of this trade-off when evaluating and deciding on policies, as they should act to reduce volatility at frequencies they are most interested in stabilizing.

Second, while policymakers have a large number of models at their disposal, none of them is the true model of the economy and none may be ideal for answering a specific policy question. Furthermore, a policy rule that is optimal in one model may perform poorly in another. The choice of model(s) thus matters and model uncertainty itself is a source of uncertainty facing policymakers. Model uncertainty has indeed played a prominent role in monetary policy analyses (see e.g. Brock et al., 2003, Levin and Williams, 2003, Levin et al., 2003, Kuester and Wieland, 2010, and Taylor and Wieland, 2012). The literature on model uncertainty identifies monetary policy rules that perform well across a variety of models, i.e. identifies rules that are robust to model uncertainty.

In this paper, we join these two strands of literature so that we can address both of the above-mentioned drawbacks simultaneously. We do so by taking a large set of structural models and looking for the model-robust rules that minimize the volatilities at those frequencies that policymakers are most interested in stabilizing.

We use several Dynamic Stochastic General Equilibrium (DSGE) models from the Macroeconomic Model Data Base, which is an archive of macroeconomic models based on a common computational platform for systematic model comparison.1 These models share antecedents and the same methodological core, but each emphasizes different transmission channels, frictions, and shocks. In particular, we use 9 models for the Euro Area and 29 models for the United States. Some of these models are currently used in policy institutions for forecasting and policy simulations (for instance, the del Negro et al., 2015 model is in use at the New York Fed).

In Figure 1 we report the distribution of optimal model-specific coefficients, the average coefficients across models (red crosses), and the optimal model-robust responses to inflation and output growth (black crosses). We plot the results for the United States models and for the central bank loss functions with variances of inflation and output growth at all frequencies (LF 5) and business-cycle frequency only (LF 6), respectively. The main results are twofold, which hold for other central bank loss functions and for Euro Area models. First, not only the average optimal coefficients across models are lower when the policymaker aims at stabilizing only some frequencies of inflation and output growth, but the entire distribution of the optimal model-specific coefficients shifts downwards. Second, the optimal model-robust coefficients are on the lower side of the boxes, thus implying a much smaller than average responses by policymakers who face model uncertainty.

Figure 1: Optimal Taylor rule coefficients (United States models)

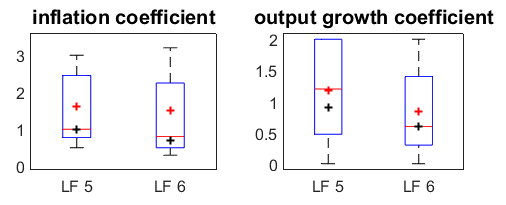
Notes. The black cross depicts the coefficients of the optimal model-robust rule, and the red cross is the average of optimal model-specific coefficients. In the box, the red line displays the median across models. The boundaries of the box depict the 25 % and 75 % percentiles. The whiskers outside of the box mark the entire range of the distribution. LF 5 and LF 6 refer to the central bank loss functions with variances of inflation and output growth at all frequencies and business-cycle
frequency only, respectively.

The policy recommendations of this paper are clear. Policymakers having preferences for stabilizing specific frequencies of inflation and output growth should react less strongly to these variables. Additional caution is needed for those policymakers who are uncertain about which structural model(s) to use.