Is there a risk of snapback in long-dated yields?

Panel remarks at the Second ECB Annual Research Conference, Frankfurt, 25 September 2017

As commentators, we give a lot of weight to market signals. We personify the market and endow it with foresight. So, when nominal yields fail to budge even in the face of impending monetary policy normalisation, we wonder what the market knows that we don’t. It almost seems as if the market is daring central bankers to follow through with their plans.

For the sake of debate, let me offer a heretical thought: what if market signals are not all they are cracked up to be? After all, the market is not a person. Prices are the outcomes of the interaction of many actors, and not the beliefs of any one actor. Speaking of the “market’s expectation” is fine as a shorthand for market prices, but perhaps we fall into the trap of taking the shorthand literally and thinking of the market as a person you can sit down and reason with.

Even as we wrestle with the question of why long-term interest rates do not budge, we know that the bond market can change course quite abruptly. Long rates overreact relative to the benchmark where long rates are the average of expected future short rates. The exact mechanism behind the overreaction varies over time and across markets, but we can sometimes shed light on what is going on without being able to predict when big market moves will happen. I will return to this at the end. In any case, looking out for potential amplification channels for long rates seems more important than ever in the current environment of low option-implied volatility in financial markets.

Let me give you an example of what I have in mind by offering a glimpse of the ultra-long segment of the euro area sovereign bond market drawing on some ongoing analysis at the BIS.2

Graph 1 overleaf shows the total holding by German residents of ultra-long bonds (remaining maturity greater than 20 years) issued by seven euro area sovereigns. The graph draws on micro data on security identifiers (ISIN) of around 600 ultra-long bonds. The left-hand panel plots how holdings of the German insurance sector have evolved over time. The bars in the chart show nominal values, not market values. Hence, shifts in the bars indicate changes in holdings, not valuation changes. The right-hand panel shows percentage holdings of these ultra-long bonds by four sectors in Germany: households, banks (monetary financial institutions (MFIs)), investment funds and insurance companies.

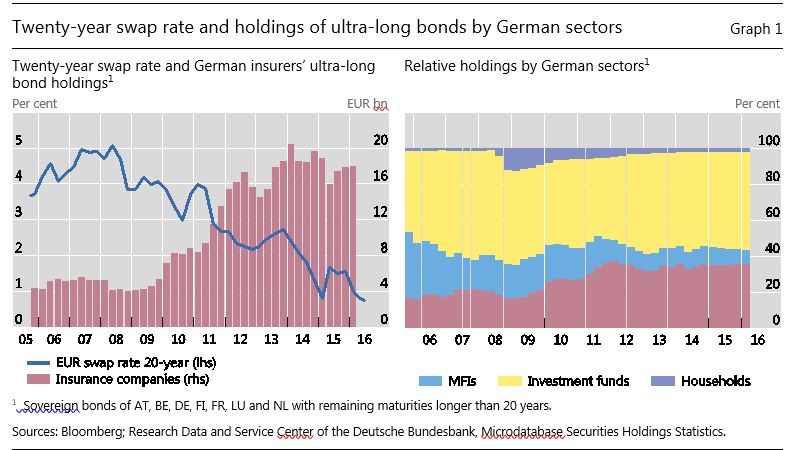
German insurance companies have more than quadrupled their holding of this subset of ultra-long bonds since 2008. For their part, German banks (MFIs) reduced their holding from €9.8 billion notional to €4 billion notional. The sharp increase in holdings of ultra-long bonds by insurers has coincided with the decline in long rates.

Life insurance companies play an important role in Germany, as they do in the euro area as a whole, as providers of long-term savings products. The important feature for our discussion is that life insurers have bond-like liabilities due to their long-term obligations to policyholders. A key concept is duration, which is a measure of how front-loaded (or back-loaded) the cash flows are. If the cash flows are in the distant future, duration is high. If they are imminent, duration is low. Duration is closely related to maturity, but is itself a price, as it depends on interest rates. Duration also measures how sensitive the market values are to changes in discount rates.3  Prudent risk management dictates that the insurance company adjusts its asset holdings so as to minimise the impact of future interest rate shocks.

Insurance obligations typically have a longer maturity profile than the fixed income assets held to meet those obligations. The left-hand panel of Graph 2 overleaf is a snapshot of the duration of European insurance companies’ assets and liabilities, taken from the 2013 stress test conducted by the European Insurance and Occupational Pension Authority (EIOPA).4

In the case of Germany, the duration of liabilities was around 20 years at the time of the survey, while duration of assets was around 10 years, meaning that liability values are much more sensitive to interest rate changes than are asset values. Prudent risk management induces the insurance company to take on additional fixed income assets to achieve overall balance as interest rates decline. Regulations may reinforce the need for such a response, but prudent risk management would suffice to elicit it.

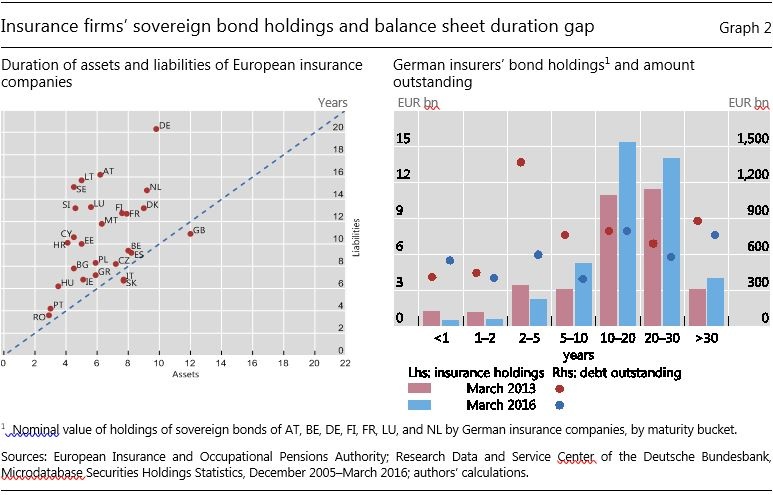
Crucially, when interest rates fall, the duration of liabilities increases faster than that of the assets. Imagine a pair of scales, with one side being the asset side and the other being the liability side. As interest rates fall, the liability side of the scales becomes heavier and tips downwards. Closing the duration gap means adding more long-dated bonds to the asset side of the scales so as to restore balance. Thus, as rates fall, the demand for long-dated bonds increases. In this way, the demand response can become upward-sloping, whereby a higher price (lower yields) elicits further purchases – a perverse response.

The right-hand panel of Graph 2 shows the maturity profile of the German insurance sector’s holdings of core euro area sovereign bonds at two dates: end-March 2013 and end March 2016. The bars represent nominal amounts, thus indicating holdings, not valuation changes. We see that holdings of longer-maturity bonds have increased. This shift came about despite no overall increase in the amounts outstanding of this subset of ultra-long bonds, as seen in the right-hand panel of Graph 2.

The key issue for market dynamics is whether the perverse demand response is strong enough to set off a feedback loop between yields and portfolio adjustment. If a sufficiently large segment of the market is chasing long-dated bonds, the market price itself may be affected. There would be an amplification cycle: a fall in long-term rates would spark even greater demand for long-dated bonds, further fuelling a decline in rates. To an outside observer, it would appear as if market participants’ preferences were changing with market prices themselves. Low rates beget low rates through higher value placed on long-dated bonds, and high rates beget high rates due to lower value placed on long-dated bonds. With upward-sloping demands, multiple equilibria could not be ruled out.

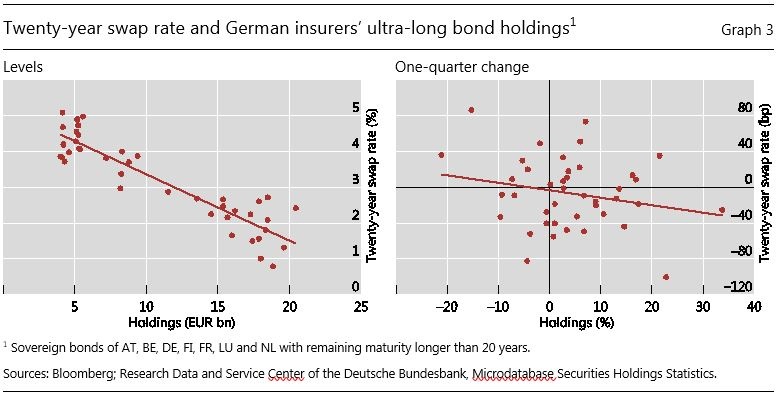
Graph 3 overleaf delves deeper into the possibly perverse nature of the relationship between bond holdings and long-dated yields. The left-hand panel of Graph 3 shows a scatter of holdings of ultra-long bonds and the 20-year swap interest rate. There is a striking negative relationship. The more expensive the bonds are, the more the insurance sector holds. The right-hand panel shows the same relationship, but in quarterly changes. The scatter chart is noisier, but the negative relationship is clear.

Three lessons

I would like to close by drawing three lessons. The first lesson is that nominal interest rates matter in their own right for bond market equilibrium, over and above their role in determining real rates. For many financial market participants, including the insurance companies examined above, the demand for long-dated bonds depends on the asset-liability mix. If the promised returns are in nominal terms, demands depend on nominal rates. The left-hand panel of Graph 3 showing the negative relationship between yields and asset holdings deserves another look.

The second lesson is that even small changes in quantities may have outsize effects on prices. We know from textbook comparative statics exercises that when the demand and supply curves both slope upwards, a small shift in the supply curve can elicit large changes in price. As central banks begin slowing their asset purchases or reducing their balance sheets outright, the additional supply will need to be absorbed. If the demand curve is upward-sloping for a segment of the market, an outward shift in the supply curve due to central bank tapering may elicit large price responses.

Term structure models offer a decomposition of long-dated yields into that part attributable to the expected path of short-term rates and the rest as the term premium.5  Nonetheless, such decomposition is only the beginning, not the end, since the decomposition only postpones the important questions. Saying that the term premium has changed is just another way of saying that the market has overreacted relative to the expectations theory of the yield curve. It still begs the question of why.

Third, and most importantly, we need to have a better understanding of the potential amplification mechanisms for long-term rates. The amplification from insurance company duration matching is closely related to other channels. A well known example is the so-called convexity risk due to the prepayment option in US mortgage contracts. US mortgage borrowers have a prepayment option, and these options are exercised when interest rates fall. Investors in US mortgage-backed securities who attempt to hedge the resulting changes in duration gaps may end up amplifying movements in long-term rates by buying long-dated treasuries when yields are falling (Borio and McCauley (1995, 1996), Fernald et al (1994), Hanson (2014) and Malkhozov et al (2016)).

Mortgage convexity hedging is probably less important now, but new amplification mechanisms spring up to take the place of the old ones. For instance, a widely discussed amplification mechanism during the 2013 taper tantrum was the activity of risk parity funds that held leveraged positions in treasuries.6 Overreactions are even more familiar in emerging market economy bond markets, associated with portfolio flow reversals (Morris et al (2017)).

We do not know what other mechanisms lie in wait for unwary fixed income investors. However, the recent paper by Hanson et al (2017) documents how the overreaction of long-dated yields over short horizons has become larger and more prevalent in recent years. It seems unlikely that we have seen the last of bond market overreactions.