Forgetting Approaches to Improve Forecasting: Executive Summary

There is widespread evidence of parameter instability in the literature. One way to account for this feature is through the use of time-varying parameter (TVP) models that discount older data in favor of more recent data. This practice is often known as forgetting and can be applied in several different ways. This paper introduces and examines the performance of different (flexible) forgetting methodologies in the context of the Kalman filter. We review and develop the theoretical background and investigate the performance of each methodology in simulations as well as in two empirical forecast exercises using dynamic model averaging (DMA). Specifically, out-of-sample DMA forecasts of Consumer Price Index (CPI) inflation and S&P500 returns obtained using different forgetting approaches are compared. Results show that basing the amount of forgetting on the forecast error does not perform as well as avoiding instability by placing bounds on the parameter covariance matrix.

Allowing for dynamics in parameters over time is currently seen as an essential component of most economic and financial models. Permitting these dynamics gives models flexibility to adapt to different regimes. An example of this is stock market predictability. During normal times evidence suggests that market returns are best modeled as `white noise’ in the sense that they do not exhibit any predictability, however during times of distress parameters governing some predictive properties change, thus illustrating some parameter variation between normal periods and time of distress. Modeling these dynamics in parameters is challenging. This challenge usually manifests itself as a trade-off between learning the wrong parameters too well or learning the correct parameters with a high amount of uncertainty. This dilemma is what this paper attempts to mitigate.

One well established method of tracking parameters in a linear model over time is by adopting a state space model, in which parameters are the unobserved state variables, and are retrieved by a methodology known as a Kalman filter. Under the assumption of a linear model with constant parameters, such as a linear regression model, the Kalman filter delivers the best parameter estimates in a minimum variance sense. However, if parameter variation is assumed, then the Kalman filter can be adapted to accommodate this by weighing recent information more than past information when estimating parameter values. This idea is known as forgetting.

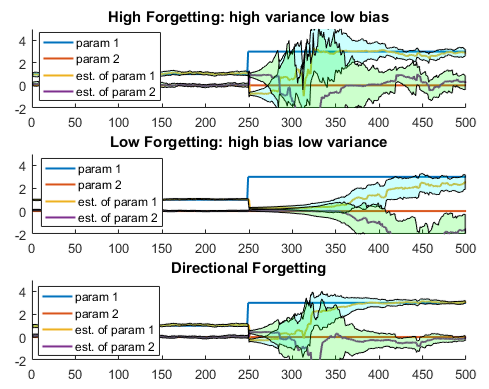
Figure 1: this figure shows true parameters in a simulated setting with their estimated counterparts. The shaded area represents the 95% confidence interval of the estimation. The top plot shows the tracking of parameters under the high forgetting specification, in which information is quickly discarded in order to allow parameters to change over time. After a shift in parameters (the blue line representing parameter 1) the system quickly adjusts, however the cost of this quick adjustment is higher variance of the estimated parameter. The middle plot gives the results from a low forgetting specification, in which there is less estimation variance albeit with slower adjustment. Lastly, the Directional forgetting scheme in the bottom plot shows quick parameter estimate adjustment with less estimation variance, thus mitigating the trade off.

Again, this forgetting presents a trade-off, forget too much and you do not have enough information to estimate parameters, forget too little and irrelevant information that pertained to a different regime, is used in estimating parameters under the current regime leading to biased estimates. Figure 1 demonstrates this trade off, by showing parameter tracking under a high and low forgetting specification. This also presents an opportunity to design a methodology that ameliorates this trade-off. For instance, in a multivariate setting, information related to some variables is irrelevant while some variables may always be relevant, identifying in which direction to forget information and where to keep it leads to less wasteful management of information and more efficient parameter estimation.

Although this idea is relatively unexplored in economics and finance, the concept of forgetting within the scope of the Kalman filter is not new. The topic has been explored in the engineering and system control literature dating from the mid 20th century. Saelid and Foss (1983), Parkum et al. (1992) and Milek (1995) have proposed algorithms that are able to discount old information which permits time variation in parameters, while ensuring that too much is not forgotten to avoid parameter estimates based on too little information. This is demonstrated in the bottom plot of Figure 1. Avoiding parameter estimation using too little information keeps estimated parameters changing, but in a stable way, which in turn has the added benefit of keeping model forecasts based on the estimated parameters less noisy. We investigate the performance of some of these proposed forgetting methods in economic and financial forecasting applications.

It is widely accepted that model averaging, or ensemble learning in a machine learning setting, leads to more accurate forecasts. This idea applied to time varying parameter models estimated via a Kalman filter has been explored by Raftery et al. (2010) and Koop and Korobilis (2012) and is commonly known as dynamic model averaging (DMA). The dynamic nature of this method refers to the change over time of the model weights in the weighted averaging procedure. The change is based on how well each individual model forecasts the target variable. If one particular model in the group of models to be averaged has a lower forecast error, it will receive a higher weight in the next model averaging step and contribute more to the overall forecast. We test the effectiveness of several forgetting schemes applied to models within dynamic model averaging

Our paper focuses on several forgetting schemes. Specifically, the directional forgetting methods proposed by Saelid and Foss (1983) and Parkum et al. (1992), as well as the stabilized linear forgetting (SLF) of Milek (1995) are analysed. The main differences between these methods is through what variables, or combinations of variables, discounting is applied in order to permit parameter variation under some constraint regarding the amount of information in the system. For example, the Parkum et al. (1992) algorithm places a minimum bound on the amount of information in the system. This is practically done by keeping the eigenvalues of the parameter covariance matrix above a certain value. As information is discarded via forgetting, parameter uncertainty grows. If left unbounded there is potential for too much uncertainty and the variance of the estimated parameters increases leading to unstable estimates and forecasts. The constraints in the Parkum et al. algorithm, and others studied in this paper are intended to avoid this. This contrasts with what is known as the exponential forgetting method that simply discounts information across all variables uniformly and has no information constraints potentially leading to noisy parameter estimates. This is sometimes known as parameter ‘blow up’ in the literature. Exponential forgetting is often used in applications with time varying parameters estimated via the Kalman filter.

We run a Monte Carlo study in order to learn more about the performance of the different forgetting schemes. In this setting it is generally found that nuanced forgetting schemes like the ones studied in this paper, work well, and give lower forecast errors compared to those of a simple forgetting method. We simulate cases in which the data generating parameters drift at the same rate, and settings in which the rates differ. As expected, exponential forgetting across all variables works well when information is being delivered uniformly into the system via the predictor variables. However, if the variances of some predictors change, the forgetting algorithms discussed above begin to outperform exponential forgetting in terms of accuracy of parameter estimates and forecast error.

We also apply the same methodology to real world data in a forecasting horserace. We forecast both US inflation and financial market returns in different out of sample periods and for different horizons. For each forecast we use a separate set of predictors, and a lagged target variable. The performance of each forgetting scheme is measured by the mean squared forecast error. For the inflation exercise at one quarter ahead forecasts, we find that more efficient forgetting schemes tend to have significantly smaller forecast errors compared with the exponential forgetting method. This presents an opportunity for forecast improvements since this method is often applied in time varying parameter models in macroeconomics. We also find that the SLF method proposed by Milek (1995) does particularly well. At four quarters ahead forecasts, the benefit of flexible forgetting schemes is less pronounced however still present. Again, the SLF approach of Milek appears to be the best performer at longer forecast horizons.

The financial forecasting results are somewhat reversed. The S&P returns are forecasted at horizons of one and four months. In this case, it is the four months ahead forecasts that appear to benefit from the forgetting scheme. The one month ahead case still has lower forecast errors however the smaller errors are not statistically significant.

To summarize, in this paper we used different means of discounting older information in favour of more recent information in the DMA procedure put forward by Raftery et al. (2010). These discounting methods, known as forgetting schemes vary from a simple fixed scalar forgetting factor that discounts uniformly across predictors, to more complicated methods that manage the information in the system more efficiently. According to our simulated and empirical applications we find that it is the specific context that will dictate which method is preferred. Our findings suggest that placing a lower bound on the amount of information in the system represented by the Kalman filter appears to work well in simulations and for forecasting inflation, as well as monthly returns at longer horizons.