Forecasting inflation with the hedged random forest

Abstract
Accurately forecasting inflation is critical for economic policy, financial markets, and broader societal stability. In recent years, machine learning methods have shown great potential for improving the accuracy of inflation forecasts; specifically, the random forest stands out as a particularly effective approach that consistently outperforms traditional benchmark models in empirical studies. Building on this foundation, this paper adapts the hedged random forest (HRF) framework of Beck et al. (2024) for the task of forecasting inflation. Unlike the standard random forest, the HRF employs non-equal (and even negative) weights of the individual trees, which are designed to improve forecasting accuracy. We develop estimators of the HRF’s two inputs, the mean and the covariance matrix of the errors corresponding to the individual trees, that are customized for the task at hand. An extensive empirical analysis demonstrates that the proposed approach consistently outperforms the standard random forest.

Forecasting Inflation with the Hedged Random Forest

Despite decades of research, improving inflation forecasts beyond simple benchmarks remains a challenge, as documented by Faust and Wright (2013). Recent work by Medeiros et al. (2021), however, shows that machine learning methods — particularly the random forest—can consistently improve forecast accuracy when applied to large macroeconomic datasets.

Building on this insight, we adapt the hedged random forest proposed by Beck et al. (2024) — a weighted extension of the standard random forest — to inflation forecasting. The method assigns non-equal, possibly negative weights to individual trees based on estimated forecast-error moments, with the aim of minimizing the mean-squared forecast error. We propose estimators for these moments tailored to time-series data. In an extensive empirical analysis using US and Swiss inflation data, our forecasts consistently outperform those of the standard random forest.

Improving Inflation Forecasts with the Hedged Random Forest

We assess the forecasting performance of the hedged random forest using FRED-MD data from 1960 to 2025.  The dataset comprises over 100 macroeconomic indicators, augmented with autoregressive terms and principal components, resulting in more than 400 predictors. Inflation is measured as the year-over-year percentage change in line with central bank practice. We consider six inflation measures: headline and core versions of U.S. CPI and PCE, and Swiss CPI. Forecast accuracy is evaluated recursively in a rolling-window out-of-sample framework (also known as a backtest analysis).

Table 1 presents RMSE and MAE ratios of the hedged random forest relative to the standard random forest, with ratios below one indicating improved performance. Both metrics — RMSE and MAE — show consistent gains of the hedged random forest over the standard random forest, with particularly large gains for core inflation measures. To evaluate whether the observed gains in forecast accuracy are statistically significant, we apply a robust version of the Diebold and Mariano (1995) test and compute a p-value for any scenario (loss function, inflation measure, forecast horizon), resulting in a total of 2 x 6 x 12 = 144 p-values. For the squared-error loss, 61 out of 72 (≈ 85%) p-values are below 0.1, whereas for the absolute-error loss, 70 out of 72 (≈ 97%) p-values are below 0.1.

Table 1. Relative Forecast Accuracy of the Hedged vs. Standard Random Forest

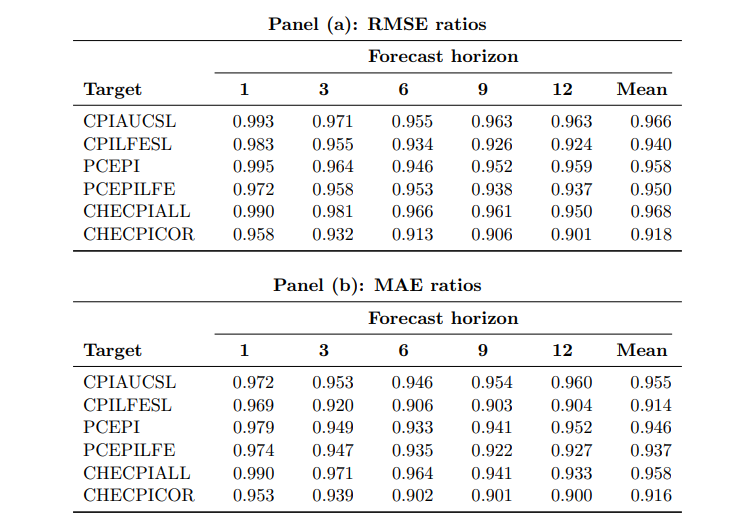
Notes: RMSE and MAE ratios of the hedged random forest relative to the standard random forest for headline and core inflation measures in the US and Switzerland evaluated across forecast horizons of 1, 3, 6, 9, and 12 months, as well as the mean over all twelve horizons (1–12). Ratios below one indicate that the hedged random forest outperforms the standard random forest.

Persistent Outperformance in Changing Economic Environments

To assess the stability of the outperformance of the hedged random forest over time, we analyze the cumulative sum of squared/absolute forecast-error differences (CSSED/CSAED) of the hedged random forest relative to the standard random forest. Figure 1 displays the corresponding trajectories, which show a persistent advantage of the hedged random forest throughout the out-of-sample evaluation period. Performance gains are particularly pronounced (i) following periods of recessions and (ii) during periods of heightened volatility, that is, precisely when accurate forecasts are most valuable for monetary policy. This pattern reflects the method’s ability to adapt to changing economic conditions and highlights its robustness across a wide range of macroeconomic environments.

Figure 1.

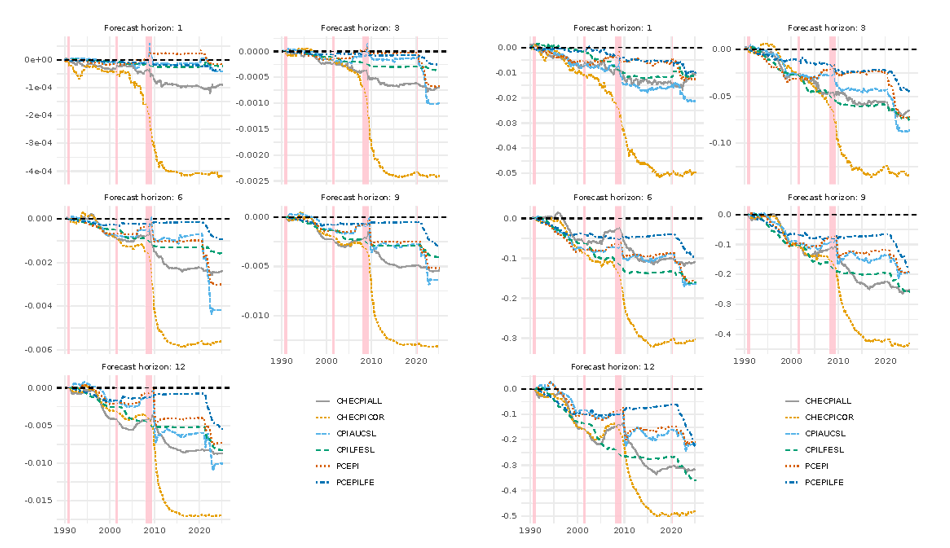
Notes: CSSED (left panel) and CSAED (right panel) trajectories of relative cumulative performance of the HRF and the RF over time, across different inflation forecast horizons and inflation measures.  Negative values indicate that the HRF has outperformed the RF in a cumulative sense until this point in time, whereas downward slopes identity periods where the HRF outperforms the RF in a local sense.