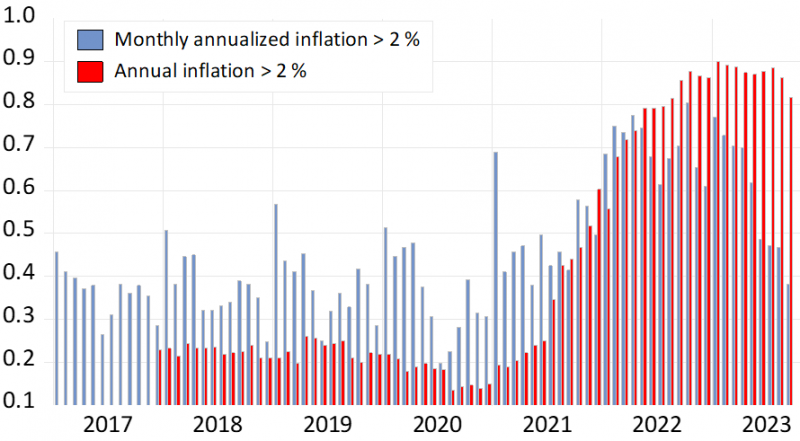
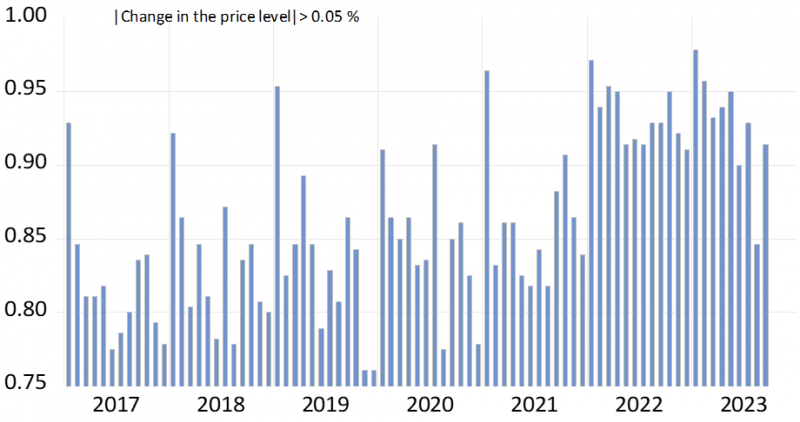
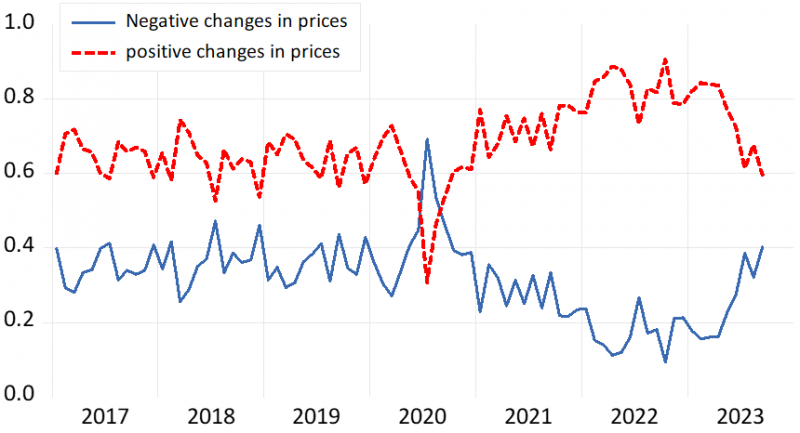
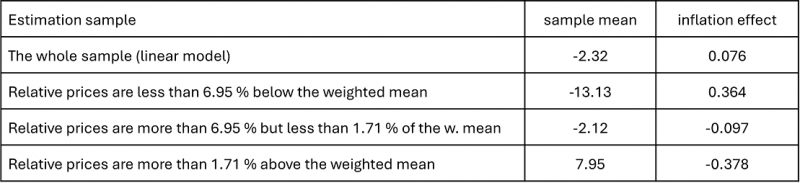
References
Bunn, N., N. Bloom, P. Mizen, Ö. Özturk, G. Thwaites and I. Yotzov (2023) Price-setting in a high-inflation environment. Vox-EU, August 7, 2023. https://cepr.org/voxeu/columns/price-setting-high-inflation-environment
Cavallo, A. (2022) More Amazon Effects: Online Competition and Pricing Behaviors. https://www.nber.org/papers/w25138
Cavallo, A., F. Lippi and K. Miyhara (2023) Inflation and misallocation in New Keynesian models. ECB Forum for Central Banking 2023. https://www.ecb.europa.eu/pub/conferences/ecbforum/shared/pdf/2023/Lippi_paper.pdf
Dedola, L., M. Kristoffersen and G. Zullig (2021) The extensive and intensive margin of price adjustment to costs hocks: Evidence from Danish multiproduct firms. https://gabrielzuellig.ch/wp-content/uploads/2021/04/CostPassthrough.pdf
Gautier, E. and H. Le Bihan (2022) Shocks versus Menu Costs: Patterns of Price Rigidity in an Estimated Multisector Menu-Cost Model, The Review of Economics and Statistics (2022) 104(4): 668–685.
Gautier, E., H. Le Bihan and F. Lippi (2023) Why prices transmit large-scale shocks more quickly. Banque de France, Post 323. https://www.banque-france.fr/en/publications-and-statistics/publications/why-prices-transmit-large-scale-shocks-more-quickly
Golosov, M. and R. E. Lucas Jr (2007) Menu Costs and Phillips Curves, Journal of Political Economy, 2007,115(2), 171-199. https://www.jstor.org/stable/10.1086/512625
Klenow, P. and O. Kryvtsov (2005) State-Dependent or Time-Dependent Pricing: Does it Matter for Recent U.S. Inflation? NBER Working Paper No. w11043, Available at SSRN: https://ssrn.com/abstract=648945
Nakamura, E. and J. Steinsson (2013) Price rigidity: microeconomic evidence and macroeconomic implications, NBER Working Paper 18705 http://www.nber.org/papers/w18705
Werning, I. (2023) Expectations and the rate of inflation. https://www.dropbox.com/s/652nw6i3cuhswpg/calvo%20conference%20inflation%20expectations.mp4?dl=0