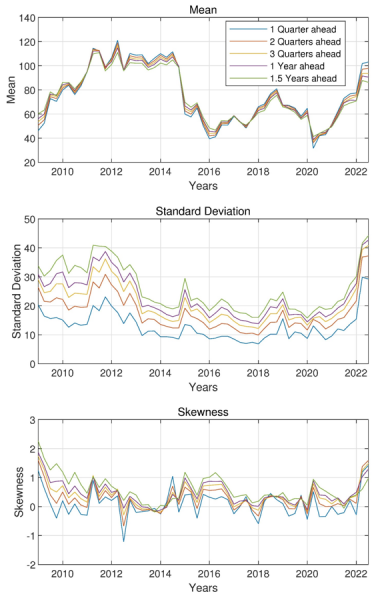
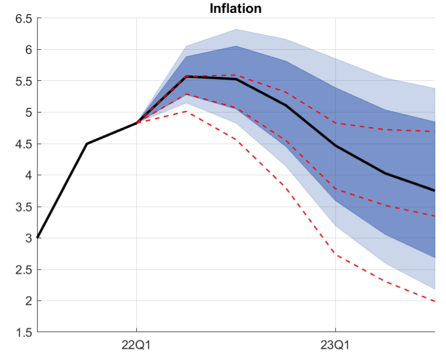
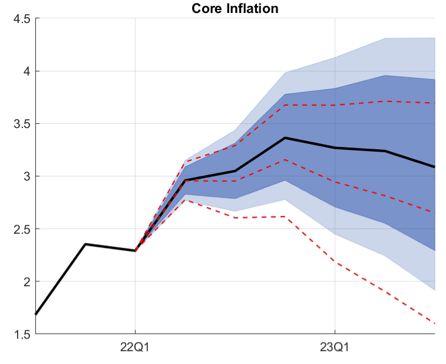
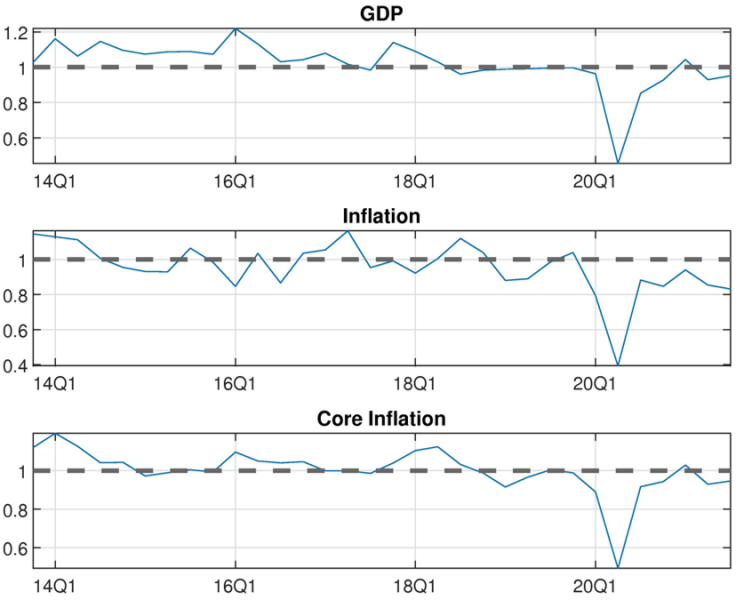
References
Coenen, Gunter et al. (2018). “The New Area-Wide Model II: an extended version of the ECB’s micro-founded model for forecasting and policy analysis with a financial sector”. ECB Working Paper No 2200.
Herbst, Edward and Frank Schorfheide (2014). “Sequential Monte Carlo Sampling for DSGE Models”. Journal of Applied Econometrics 29(7), pp. 1073–1098.
Herbst, Edward and Frank Schorfheide (2019). “Tempered particle filtering”. Journal of Econometrics 210(1), pp. 26–44.
Neal, Radford (2001). “Annealed importance sampling”. Statistics and Computing 11, pp. 125– 139.